ミニセミナー・基礎講座
分析・評価・解析
目次
評価・分析・解析
評価・分析・解析
AFMによる微細加工パターンの付着性解析(1)
電子デバイスの発展とともに、シリコン材料を主体とした微細加工技術(リソグラフィ)が進展してきた。基板のエッチングには、高分子材料を主体としたマスクが用いられる。デバイスの設計ルールの縮小化に伴い、高分子パターンと基板との付着性の確保が重要となってきている。微細領域でのパターン付着性は、原子間力顕微鏡(AFM)を用いて直接解析できる。ここでは、河合研究室が開発した付着力解析法と事例を紹介し、その有効性を検証する。

レジストパターン(60nm線幅)
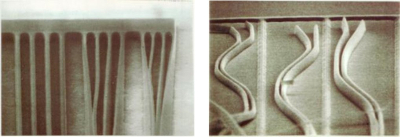
IT産業の発展上、今後、電子デバイスに用いられる微細加工技術は、ナノサイズをクリアすることが求められる。そのために、様々なリソグラフィ技術が開発および実用化されつつある。右図は、電子線(EB)で描画して作製した線幅60nmのライン高分子パターンを示している。このような微細サイズになると、形状観察や品質管理などにおいて、高分解能の電子顕微鏡や走査型プローブ顕微鏡(SPM)が必要になり、高分子材料開発だけでなく周辺技術の進歩も重要な要素となる。しかし、下図のように、現在のリソグラフィプロセスでは、微細高分子パターンの基板からの剥離が問題になっている。このパターン剥離は、パターンを現像する際のリンス処理において、パターン間に存在するリンス液(純水)のラプラス力に起因している。また、この剥離したパターンは、その後のエッチングマスクとしては不十分であり、デバイス不良の原因となる。近年では、現像工程だけでなく、その後の真空下で行われるエッチング工程でもパターンが剥離する。よって、高分子パターン自体の凝集性を高め、剥離要因に対する機械的な強度の確保が重要となる。ここで、高分子パターンの剥離現象に関与する要因を考察する。物理的要因として、高分子材料、高分子基板界面、基板材料などにおける複数の要因が同時に関与する。付着性の改善には、これらの要因を定量化し解析することが重要になる。現在のところ、高分子パターンの剥離現象は、関与する要因の多さに比べて、得られる実験的情報が少ないため解決に時間がかかる。
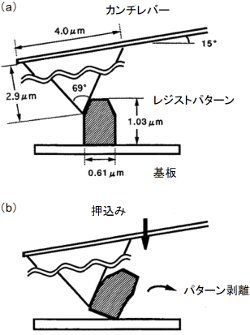
河合研究室では、AFMを用いて、微細高分子パターンの付着性および凝集性の定量的な解析技術を開発している。右図はAFMによる高分子パターンの剥離試験(DPAT:Direct Peeling method by using AFM Tip)法の概略を示している。AFMの微細探針を用いると、パターン上の任意の場所に直接荷重を加えることが可能となり、かつ、その場観察でパターンの剥離性を解析できる。まず、(a)のように、AFMにより高分子パターンに荷重を加えずに形状を観察する。この像から、パターン内の荷重印加点を決定する。この場合、高分子パターンおよび探針には、変形およびクラック等は生じさせない。次に、(b)において、探針の先端をパターン上の荷重印加点に接触させて、パターンに荷重を加える。このとき、カンチレバーの変位は光学系により制御されている。探針を移動させて荷重をさらに加えることでパターン変形および剥離が生じる。この場合に探針から加えられた荷重は、探針の変位とばね定数から換算できる。最終的に、基板からのパターンの剥離および高分子残渣形成を確認する。このように、本手法は、微細パターンに直接荷重を加えて、付着・凝集特性を解析できることが特徴である。次に、AFMによって測定した微細高分子パターンの付着・凝集性の具体例を示す。


SEM写真(4万倍)
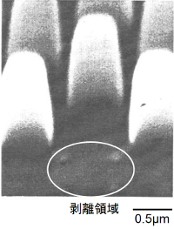
ここでは、365nmの紫外線(i線)に感度を有するポジ型高分子材料を使用して微細パターンを作製した。この高分子パターンは、ノボラック樹脂、感光剤、溶剤の3成分から成っている。一辺600nmの正方形マスクパターンを高分子膜中に転写し、TMAH(tetramethylammoniumhydroxide)2.38%水溶液中に浸し、露光部の溶解除去を行った。そして、熱処理は150~300℃までの各温度でホットプレートを用いて5分間行い、高分子パターン全体を硬化させた。上の左図はAFMにより観察した高分子パターン配列を示している。リソグラフィで作製したパターンが規則的に配列している様子が分かる。上の左図は、DPAT法によるパターン破壊時の感度を検証している。この場合のパターンの剥離荷重は7.040nNであったが、6.953nNの荷重の場合はパターンの倒壊は生じていない。よって、本手法を用いた付着荷重の測定分解能は約0.08nNであるである。これは付着力試験法としては、高い分解能である。右図は、基板から剥離した高分子パターンのSEM像を示している。個々のパターンが倒壊している様子が分かる。また、ほとんどのパターン倒壊は基板上に残さを形成しないため、高分子材料の凝集破壊は生じていない。下の左図は、高分子パターンの剥離荷重の熱処理温度依存性を示している。DPAT法による試験では、熱処理温度の増加に従い剥離荷重(●)も増加しているため、高分子パターンと基板との付着力の増大を表している。実験的には、約3桁の付着力増加が確認できる。この付着力の増大は、表面エネルギーの増大やフォト高分子材料の硬化などが顕著に反映している。従来の付着力評価法である引張り破壊試験の結果(○)も、DPAT法と同じ傾向を示しているが、付着力の増加は1桁程度である。これは、下の右図にあるように、破断面が界面破壊と凝集破壊の混合破壊となるため、測定感度が鈍ったことに起因する。よって、局所測定であるDPAT法では、測定感度も増加させる効果がある。
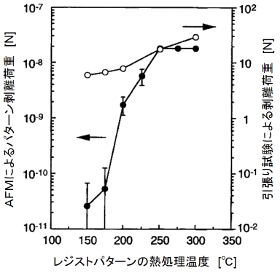
レジスト熱処理温度依存性

ここでは、AFMを用いたナノスケールの微小固体の付着・凝集および表面特性解析について述べた。AFMの微細探針を用いて荷重を加えるDPAT法により、微細高分子パターンの付着力解析を定量的に解析することができる。
参考文献
- Binnig. G, Quate. C. F and Gerber. Ch; Phys. Rev. Lett, 56, 930 (1986).
- Akira Kawai, "Collapse Behavior of Micro Resist Pattern Analyzed by Tip Indentation Method with Atomic Force Microscope", J. Vac. Sci & Technol. B17, 1090-1093 (1999).
- 河合 晃, "原子間力顕微鏡(AFM)を用いた微細探針走査法によるフォト高分子微細パターンの接着性解析", 日本接着学会誌、36, 2-9 (2000).
AFMによる微細加工パターンの付着性解析(2)
原子間力顕微鏡(AFM: Atomic force microscope)を用いて、サブミクロンサイズのフォトレジストパターンの接着および凝集性解析を試み、この手法の妥当性を議論する。フォトレジストパターンとして、平坦基板上の高さ1.01μm、幅0.60μmのドット形状のものを一個選択し、微細探針から直接荷重を掛けながら走査することで倒壊させる。そして、倒壊に要した荷重、および倒壊直前のパターン歪みを測定する。このパターン歪み測定と有限要素法による応力変形解析との組み合わせにより、界面剥離を引き起こす要因となった内部応力およびパターンのヤング率を算出する。これらの値は、フォトレジストパターンの熱処理温度の増加に伴って大きくなることが分かった。この傾向は、フォトレジスト膜の熱重量(TG)と硬度および屈折率などの熱処理温度依存性と密接な相関を示しており、本手法の妥当性を確認した。本手法は、フォトレジストパターンなどの微細構造体の接着および凝集特性を直接解析する上で有効である。
リソグラフィ技術のエッチング用マスクとして用いられるフォトレジストの微細パターンのように、基板上に形成された微細な高分子凝集体の接着力改善が重要な課題となりつつある。特に、半導体集積回路および液晶表示素子などに代表される電子デバイスでは、集積化が促進されることによりデバイス作製時の加工寸法もサブミクロンに達している。このような微細な寸法になると、ウエット処理時にフォトレジストパターン間に働くラプラス力の影響が大きくなり、パターン剥離などの問題が生じてくる。また、今後はKrFおよびArFエキシマーレーザーを光源とする光リソグラフィ技術の進歩により、0.1μm線幅クラスのフォトレジストパターンの接着安定性が要求されている。特に、21世紀には0.1μm以下の線幅のフォトレジストパターンが実用化されると考えられている。しかし、現在では、ミクロンスケールの構造物の接着、凝集および破壊特性などを直接解析する手法は少なく、バルク的な固体の物性値を用いて解析が行われている。しかし、1986年にBinnigらにより原子間力顕微鏡(AFM:Atomic force microscopy)が開発されて以来、表面科学における解析精度は大幅に改善されてきた。また、近年では、解析対象は分子および原子スケールにまで至るとともに、それらの加工技術の確立、新材料および新技術の出現が期待されている。
レジストパターンの作製には、365nmの紫外線(i線)に感度を有するポジ型フォトレジストを使用した。このフォトレジストは、ノボラック樹脂、感光剤、溶剤の3成分から成っている。ノボラック樹脂の熱軟化温度は約150℃である。感光剤はナフトキノンジアジドであり、分解温度は135℃である。溶剤はエチルセルソルブアセテートであり、沸点は156℃である。フォトレジスト膜は、スピンコート法により1.01μmの膜厚でSi(100)単結晶基板上に形成した。その際、シランカップリング処理などの密着強化処理は施していない。その後、紫外線露光装置(日本光学工業(株)、NSR1505-i3)を用いて、一辺0.60μmの正方形マスクパターンをフォトレジスト膜中に転写した。そして、フォトレジスト膜をTMAH(tetramethyl-ammoniumhydroxide)2.38% 水溶液中に浸し、露光部の溶解除去を行った。引き続き、イオン交換水中に3分浸漬しリンス処理を行った。試料の乾燥後に遠紫外光(波長0.3μm以下)を照射し、フォトレジストパターンの表面層の硬化処理を行った。これにより、続いて行う熱処理時に生じるパターン変形を防ぐことが出来る。熱処理は150~300℃までの各温度でホットプレートを用いて5分間行い、フォトレジストパターン全体を硬化させた。
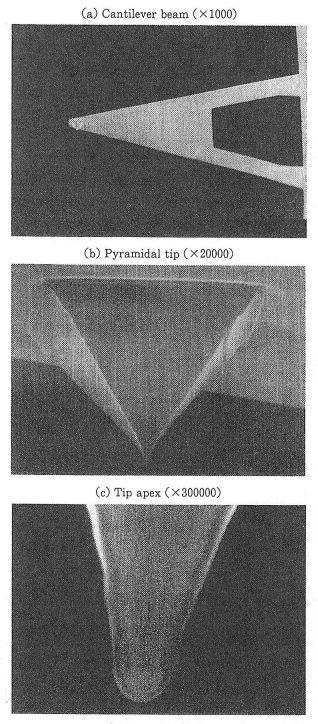
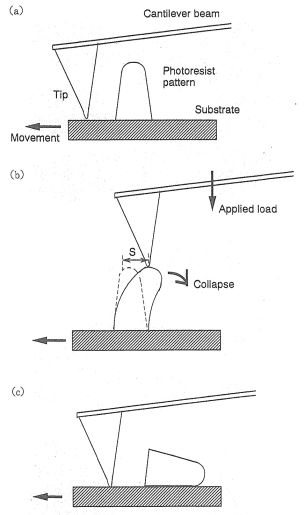
フォトレジストパターンの歪み測定には、AFMの探針と試料表面が常に接触するコンタクトモードを使用した。使用したカンチレバーの材質はSi3N4膜であり、長さは200μm、厚さは20μmのものを用いた。その先端には、長さ20μmで先端曲率半径が25nmのピラミダル型の微細探針がマウントされている。探針の先端角は69°である。使用したカンチレバー、探針および探針先端の電子顕微鏡(SEM)写真を下の左図(a)~(c)にそれぞれ示す。フォトレジストパターンの歪み測定は、下の右図(a)~(b)に示すような測定フローにより行う。(a):低荷重(0.01nN)において変形前のフォトレジストパターン像を測定する。この時、パターン変形は殆ど生じていない。(b):探針に荷重をかけながら基板を横方向に移動させることにより、フォトレジストパターンを変形させる。この時、探針から加える荷重は常に一定値になるようにフィードバック制御されている。フォトレジストパターンが倒壊する直前の歪みSを、測定したパターンプロファイルから求める。(c):再び低荷重を掛けながら試料表面像を測定し、フォトレジストパターンの倒壊および剥離を確認する。
測定したフォトレジストパターンの歪みとカンチレバーにより加えた荷重に基づき、有限要素法を用いてフォトレジストパターンの内部応力分布およびヤング率を各熱処理温度に対して算出した。この時、有限要素解析の分割数は120個、フォトレジストのポアソン比は0.33とした。また、フォトレジストパターンと基板との界面は、固定点として扱った。そして、実験により測定したフォトレジストパターンの歪みと変形解析による歪みが一致する様にヤング率の値を変えて計算した。そして、最終的にフォトレジストパターンの内部応力分布および変形像を決定した。
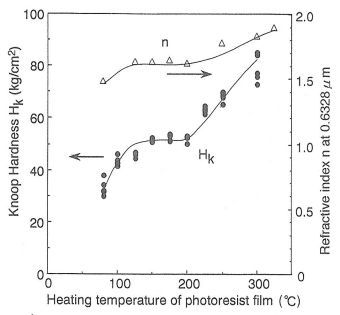
熱処理に伴うフォトレジスト材料の熱重量、硬度および屈折率を測定した。熱重量は、セイコー電子工業(株)製の熱重量測定装置を用いた。フォトレジスト膜の硬度は、ヌープ硬度計(明石工業(株)製、MKV-G2)を用いて測定した。荷重範囲は、0.5~20gfであった。屈折率はエリプソメーター(ガートナー社製)を用いて、He-Neレーザー(波長632.8nm)の屈折率を測定した。

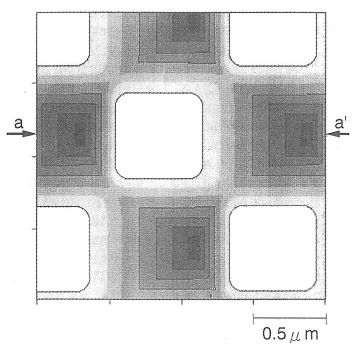
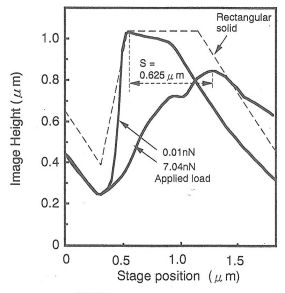
上の左図(a)と3(b)には、各荷重におけるフォトレジストパターンのAFM像を示している。上の左図(a)のように、0.01nNの低荷重を掛けた場合はフォトレジストパターン配列が確認できる。図において、探針は左から右へ走査しながらパターン像を測定している。しかし、この時のパターン像は、AFMの微細探針の先端形状(ピラミダル)が反映されて歪んだものになっている。そこで、理想的な直方体パターンにピラミダル形状の探針が接触した場合のパターンプロファイルを数値解析により求めた。上の右図は、高さ1.0μmで0.6μm角の直方体パターンについて得られるプロファイルを示している。等高線の間隔は、0.12μmである。このように、直方体でのパターンプロファイルは、上の左図(a)のパターン像をほぼ反映していることが分かる。一方、上の左図(b)の7.04nNの荷重を掛けた場合では、中央のフォトレジストパターンが探針走査の途中で剥離倒壊したことによって、観察像が乱れていることが分かる。また、この時よりもわずかに低い荷重である6.91nNの場合では、フォトレジストパターンが倒壊せずに残っていることを確認している。よって、フォトレジストパターンの倒壊時の荷重は7.04nNであることが分かる。また、本手法を用いた場合の倒壊時の荷重の測定分解能は、約0.1nNであることも分かる。これは非常に高い分解能であるといえる。下の左図には、倒壊によって基板から剥離したフォトレジストパターンのSEM像を示している。個々のパターンが倒壊していることが明確に分かる。また、ほとんどのパターンは元の形状を維持しており、凝集破壊は生じていないことが分かる。次ぎに、フォトレジストパターンの倒壊直前のパターン歪みSを測定する。下の右図は、各荷重におけるフォトレジストパターンのAFM像の断面プロファイルを示している。また、上の右図の直方体パターンの(a-a’)ラインにおける断面プロファイルも図中に示している。0.01nNの低荷重を加えた場合には、フォトレジストパターンの歪みは殆ど見られていない。しかし、微細探針から7.04nNの荷重を掛けることにより、パターンプロファイルは走査方向に大きく傾きパターン歪みが生じているのが分かる。この時のパターン歪みSは、0.625μmであると見積もることが出来る。一方、7.04nNよりも低い荷重では、荷重を取り去った後のパターン像に変形および位置ずれが全く見られないことから、これらのパターン変形は弾性領域で生じたと考えられる。

SEM写真(4万倍)
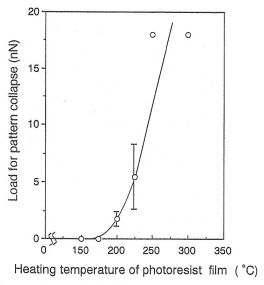
右図には、パターン倒壊に要した荷重の熱処理温度依存性を示している。熱処理温度の増加に従い倒壊に要する荷重も増加することから、フォトレジストパターンと基板との接着力が増大していることが分かる。これは、マクロなサイズでの評価法である引っ張り破壊試験の結果とも対応している。
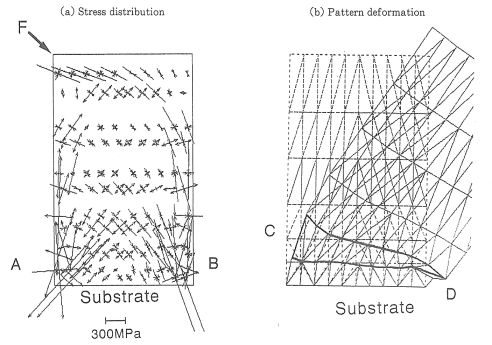
下図(a)と(b)には、有限要素法により計算したフォトレジストパターン断面における内部応力分布と変形解析結果をそれぞれ示している。下図(a)の内部応力分布において、基板との界面付近で引っ張り応力(A点)および圧縮応力(B点)が集中していることが分かる。また、パターンの内部よりは表面に近いほど応力が大きくなる事が分かる。パターン倒壊は、この内部応力分布に従って生じると考えられる。一方、下図(b)のパターン変形図において、基板との界面よりも僅かに上部のC及びD点において、パターンの伸びおよび収縮が最も顕著になることが分かる。ここで、CおよびD点での破壊限界がレジストパターンと基板間の接着力より低い場合には、パターン倒壊時にフォトレジストパターンの凝集破壊がこれらの点で生じ、基板上に残さが形成されると考えられる。また、逆に、破壊限界が高い場合はパターン倒壊が界面破壊によって生じると考えられるため、残さは生じない。本実験においては、図5のパターン倒壊後のSEM写真において、基板表面に顕著な残さが認められない。よって、フォトレジストパターンの凝集性が高く、パターン倒壊は界面破壊で生じたと考えられる。この傾向は、熱処理の全温度範囲において確認している。
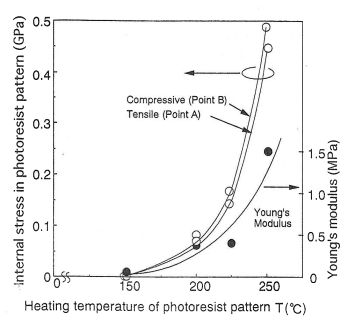
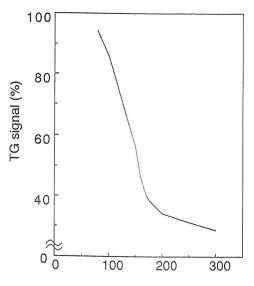
右図は、上図(a)に示されたA点およびB点における内部応力とフォトレジストパターンのヤング率の熱処理温度依存性を示している。図より、熱処理温度の増大とともに最大応力が大きくなることが分かる。この内部応力の増大は、熱処理によるフォトレジスト材料の硬化などが顕著に反映したものと考えられる。下の左図には、フォトレジスト材料の熱重量(TG)の測定結果を示している。溶剤の沸点である156℃まではレジスト膜内の残留溶剤量は急激に減少するが、200℃以上では残留溶剤の蒸発がほぼ完了することが分かる。また、下の右図にはフォトレジスト膜のヌープ硬度と屈折率の熱処理温度依存性をそれぞれ示している。フォトレジスト膜のヌープ硬度および屈折率も200℃以上で大幅に増加しており、熱処理によってフォトレジスト材料の熱硬化が生じているのが分かる。以上の結果より、熱処理温度の増加に伴いフォトレジスト材料の硬化反応が進み、フォトレジストパターンの凝集力が増したことが分かる。この点からも、図7のフォトレジストパターンの接着特性が界面破壊であることを説明できる。一方、図9にあるように、フォトレジストパターンのヤング率も内部応力と同様な熱処理温度依存性を示している。フォトレジストパターンのヤング率は1MPa前後の値となったが、これは弾性ゴムのヤング率(1.5~5.0MPa)に相当する低い値である。この理由として、フォトレジストパターンへの現像液およびリンス溶液の浸透、およびそれに伴うレジスト樹脂の膨潤などが考えられる。特にTMAHなどのアルカリ水溶液は、フォトレジスト膜中に容易に浸透し、膜応力等の物性値を容易に変化させる事が分かっている。
これまでにも微細凝集体の凝集特性に関する研究は数多くなされている。Johansson及びWillsonらは、Siの微細カンチレバーを作製して押込み変形法でヤング率を測定した。そして、Siの微細カンチレバーの破壊限界は、材料の結晶性とサイズに大きく依存していることを示した。また、Matthewsonらは、平坦面への微小球の押込み方法により、無機固体表面の微小領域の弾性特性を解析している。このように、微細凝集体の凝集特性の研究は、無機および金属材料を中心に行われてきたといえる。しかし、本研究のように凝集性の低い高分子材料の微細構造体の研究には、AFMなどの精密な制御機能が必要になってくる。また、AFMを用いた本技術の測定精度は、ピエゾステージの移動精度およびカンチレバーの撓み量の検出精度によって主に支配される。図7にもあるように、測定値のばらつきはある程度認められるが、接着現象の基本的解析には十分であると考えられる。また、本手法の課題としては、微細探針とフォトレジストパターン表面との間に生じる摩擦力や実効接触面積の定量化、および帯電、吸着水の影響の除去などがある。著者らは既にフォトレジスト膜表面の摩擦力の熱処理温度依存性を示しており、微細探針の走査速度およびフォトレジストの熱処理温度の違いによって影響を受けることを確認している。また、微細探針とフォトレジスト膜との接触による接触面積も熱処理温度によって変化することが分かっている。特に、フォトレジスト膜の表面は軟化温度である150℃付近で軟らかくなり、微細探針が膜表面へ押込まれる可能性がある。一方、本手法によれば、溶液中での微細パターンの接着挙動解析も可能であり、接着界面における溶液の浸透力解析などに有効であると考えられる。また、本手法は、微粒子の付着凝集解析およびマイクロマシンなどの微細デバイスの構造強度解析など、今後多くの分野へ適用できるものと考えられる。
原子間力顕微鏡(AFM)を用いた微細探針走査法により、サブミクロンサイズのレジストパターンの接着および凝集性を解析した。実験では、フォトレジストパターンの熱処理温度を変えながらパターン倒壊に要する荷重を測定し、破壊挙動を解析した。本研究により、以下の事が明確になった。
(1)フォトレジストパターンの倒壊は、約0.1nNの荷重分解能で解析できる。
(2)フォトレジストパターンの接着不良は、基板との界面破壊によって主に生じる。
(3)有限要素法との組み合わせで、フォトレジストパターンのヤング率や内部応力分布などを直接解析できる。
本手法は今後の微細デバイスや微細凝集体の接着および凝集挙動解析に有効である。
AFMによるナノ気泡・ナノ液滴解析
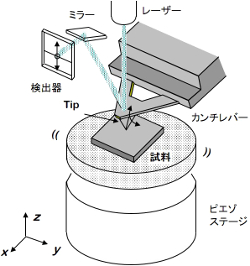
通常、液中での気泡観察に、光学顕微鏡がよく用いられる。しかし、その解像限界は約0.5μm程度であり、それより小さいサイズは観察できない。また、レーザー散乱法によって、液中の気泡数をカウントする装置も存在するが、気泡形状までを把握することはできない。そこで、AFMを用いることにより、光学顕微鏡では観察できなかったナノ気泡を解析することが可能となる。河合研究室ではこれまでに、様々なナノ気泡の観察を行ってきた。右図にはAFMの基本構造を示している。AFMはナノスケールで制御できるピエゾステージ、気泡を検出するカンチレバー、カンチレバー変位を検出する光学系から構成されている。カンチレバーの先端には、微弱な相互作用を検出するためのAFM探針が装着されている。最近は低価格のAFMもあり、教育機関での実験・実習にも幅広く取り入れられている。下図は、基板上に付着したナノ気泡のAFM像を示している。一般に、AFMで観察できる像は、気泡と微粒子(固体)との区別がつきにくい。実際には、両者ともよく似た凸像として観察される。このナノ気泡の同定には、AFMの探針と気泡間に生じる相互作用力を用いる。これには、フォースカーブと呼ばれる特性を、気泡と固体に対して測定する。

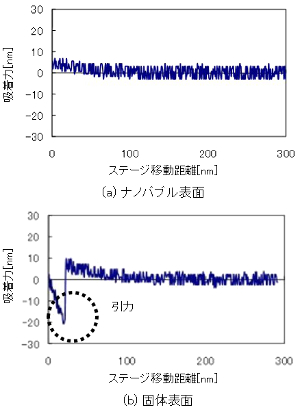
右図には、ナノ気泡上と固体表面で測定された液中のフォースカーブを示している。ナノ気泡上には僅かに斥力が働いているが、固体表面では大きい引力が作用している。これは、Lifshitz理論によって、気泡と固体表面の相互作用力に差が生じることで説明できる。下図には、この場合の測定系の構成を示している。ここで、注目するのは、探針/純水/気泡、あるいは固体の系である。すなわち、系の屈折率の大きさが順序になっている場合は斥力が働き、それ以外の系では引力となる。液中の気泡観察のケースは、相互作用力が正の値となり斥力となる。よって、AFMでの像取得後に、像中心における相互作用を測定し、その斥力および引力を解析することでナノ気泡の同定ができる。このように、AFMはナノスケールでの微小気泡の付着凝集挙動の解析に有効な機器となることが分かる。
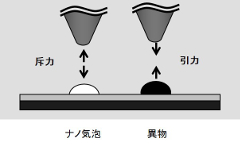
以上のように、AFMを用いることで、ナノ気泡の形状を明らかにできる。ここでは、さらにAFMの特性を活かし、ナノ気泡の付着特性を解析する。河合研究室ではこれまでに、AFMを用いて、微小パターンや微粒子などの付着性を解析するDPAT法(Direct Peeling Method by using AFM Tip)を確立し、微小気泡の付着凝集性の解析へ適用してきた。下図は、レジスト膜上に付着したナノ気泡のAFM観察像である。ここでは、これらのナノ気泡にAFM探針をアプローチして、分離と移動を試みる。AFM探針の制御により、ナノ気泡を分離して移動させた様子も示している。ナノ気泡の分離に要した力をフォースカーブにより解析すると、約3nNとなり非常に微弱な力であることが測定できた。このように、ナノスケールでの微小気泡の制御においても、AFMは有効な解析手段といえる。
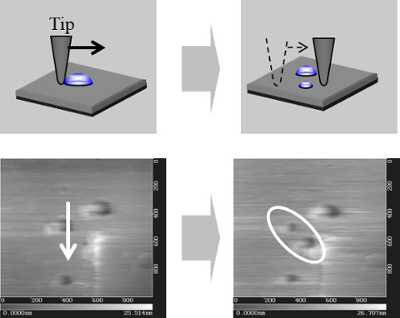
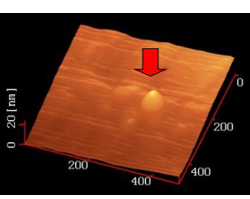
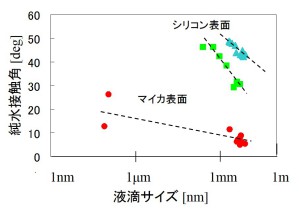
AFMを用いて、ナノ気泡だけではなく、ナノ液滴の観察が可能である。下の左図はマイカ(雲母)板のへき開表面に、飽和水蒸気下の環境で凝縮して形成したナノ液滴の観察像である。マイカのへき開表面は結晶格子間の結合力の弱い面が破壊するため、結晶面が露出し極めて平坦な表面となる。よって、基板の表面凹凸ではなく、明確にナノ液滴を確認することができる。観察できたナノ液滴のサイズは119nmであり、接触角は26度である。このように、ナノサイズ領域においても液滴は形成されるため、熱力学的な取り扱いが可能である。ただ、ここでもサイズ効果を考慮する必要がある。下の右図は、純水液滴のサイズ依存性を示している。基板はマイカとSi基板である。液滴サイズの減少とともに、接触角が増大する様子が分かる。これは、サイズの縮小に伴い、表面特性が優勢となるため、液滴がより球形に変形するように働くためである。よって、表面張力は同じであっても、液滴サイズが小さくなると、濡れ性が低下することを示している。そのため、微細加工を主体とする製品などは、さらに濡れ性が低下するため品質への影響を考慮する必要がある。ここでは、ナノスケールの物質に対する取り組みにおいて、AFM解析の有効性を示した。
参考文献
- Akira Kawai, "Condensation Behavior of nanoscale bubbles on ArF excimer resist surface analyzed by atomic force microscope", J. Photopolymer Sci. Techno.,, 18(3), 349-354 (2005).
- Akira Kawai, "Removal mechanism of nano-bubble with AFM for Immersion Lithography Microelectronic Engineering", 83, 655-658 (2006).
- Akira Kawai, "Condensation Mechanism of Micro Bubbles Depending on DFR Pattern Design", Microelectronic Engineering, 83, 1167-1169 (2006).
AFMを用いた微小固体のヤング率測定

(直径85nm)
高分子パターンの強度設計のために、パターン自体の機械的特性を直接測定する必要がある。特に、固体材料のヤング率(弾性率)は、変形・硬さ・破壊を解析する上で重要な物性値である。ヤング率の測定は、通常、薄膜あるいは棒状の試料を用いて応力-歪特性から求める。しかし、微細な高分子パターンのヤング率を実測することは困難であった。ここでは、AFM探針を用いて基板上に形成されている高分子パターンに直接荷重を加えることでヤング率を実測する。右図には、高分子パターンの電子顕微鏡(SEM)写真を示している。この高分子材料の主成分はスチレン系の樹脂である。この高分子パターンは、円筒形に近い形状を有しており、ヤング率測定に適している。
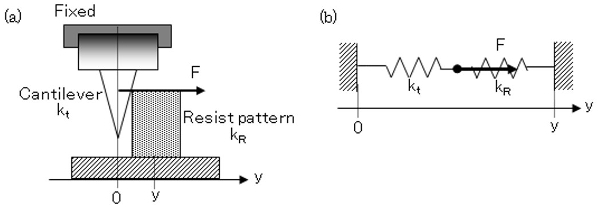
まず、AFMを用いて高分子パターンのヤング率を直接解析する手法について述べる。上図に、高分子パターンのヤング率解析の概要を示している。AFM探針と高分子パターンを連結ばねモデルとして近似することで、弾性特性を解析している。これによると、系全体のばね定数ktotalは下式(1)のように表すことができる。
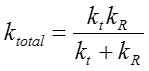 (1)
(1)
但し、
![]()
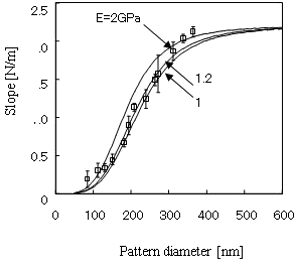
ここで、kt はカンチレバーのばね定数、E は高分子パターンのヤング率、I は断面2次モーメント、 l はパターン高さである。AFM探針により直接荷重を加えた場合のパターンの変形特性を連結ばねモデルに基づき解析する。右図は、円筒形の高分子パターンに対してヤング率を解析した結果を示している。図中、曲線は式(1)で得られる基本特性であり、高分子パターンのヤング率をパラメータにして計算されている。これにAFMで実測したパターン変形率をプロットすることで、高分子パターンのヤング率を求めることができる。右図の場合、高分子パターンのヤング率を1.2GPaとして決定することができる。この値は、ポリスチレン(2.7~4.2GPa)、ポリエチレン(0.4~1.3GPa)などの高分子材料に近い値である。
今後、高分子パターンのようなミクロな構造体の物性および特性の信頼性の確立が求められるAFMに代表される微細領域での解析技術の重要性は、さらに高まると考えられる。
参考文献
- Akira Kawai, Norio Moriike, "Adhesion and Cohesion Analysis of ArF/SOR Resist Patterns with Microtip of Atomic Force Microscope (AFM)", J. Photopolymer Science and Technology, 14, 507-512 (2001).
相互作用力を実測し付着力を推定する
界面の付着とは、付着要因と剥離要因とのバランスに基づく安定状態を意味する。付着状態を維持するには、付着要因が優勢となる必要がある。付着力の起源は、表面に存在する分子間の相互作用に起因する。溶剤を蒸発させる程度の熱処理では、表面間の化学結合は生じにくい。そのため、付着力を増大させるには、作用する表面の分子数密度と分極率を高め、かつ、相互作用距離を短くすることが効果的である。ここでは、界面の付着現象をミクロレベルに掘下げて、その要因を解析する。また、界面の実効接着面積について考察する。さらに、原子間力顕微鏡(AFM)を用いて、実際の表面間の相互作用力を解析し、未知の表面間の付着力を予測する。
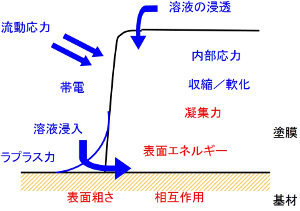
界面の付着要因には、水素結合やファンデルワールス力に代表される分子間力、表面エネルギー、表面の凹凸に起因するアンカー効果、境界水に働くラプラス力などがある。また、剥離要因には、熱膨張の差に起因する熱応力、結晶格子の界面歪みによる真応力、界面のナノ空隙、塗膜への溶液浸透などが考えられる。これらの要因が単独で作用することは少なく、複数の要因が同時に作用する。界面の付着状態は、右図のように、付着要因が優勢であれば維持され、剥離要因が上回れば界面は分離する。これらの要因は、単位面積当たりのエネルギーとして解析し、定量的な界面評価が可能である。付着トラブルの対応策として、付着力の増大よりも、応力などの剥離要因の緩和が効果的であるケースが多い。また、塗膜や基板の凝集破壊が剥離原因である場合、基板の表面処理は効果的でない。よって、付着トラブルが生じた場合、剥離界面の観察を最優先し、破壊起点や剥離モードなどのデータ収集がトラブル解決策に必要である。
基板上に塗膜がコーティングされると、その付着界面を観察するのは難しい。通常、付着面積は塗膜と基材の接触面積が用いられる。しかし、塗膜界面の全てが付着に寄与しているとは限らない。ここでは、付着界面を詳細に観察する。下の左図は、原子間力顕微鏡(AFM)の微細探針を用いて、シリコン基板上に形成された微細レジストパターンを倒壊させた写真である。レジストパターンの線幅は0.6μmで高さは1.0μmである。このレジスト材料は、ノボラック樹脂、感光剤、溶剤の混合物である。パターン倒壊により、これまで観察できなかったパターン底面が確認できる。パターン底面には微細な窪みが多数存在しており、これらの構造は基板との界面付着に影響すると考えられる。パターンが付着していたSi基板表面にはレジスト残さはないため、パターン倒壊はパターンの凝集破壊に起因するものではない。すなわち、塗膜の乾燥時に残留溶剤が蒸発した際に、このようなポーラス構造が形成されたと考えられる。界面にポーラス構造が存在すると、下の右図のように、基板との相互作用距離が局所的に長くなり、界面の付着に寄与しなくなる。よって、レジストパターンとシリコン基板間の実効付着面積は低くなる。下の左図の場合の実効付着面積は50%程度である。次に、原子間力顕微鏡(AFM)を用いて、界面における相互作用力および付着力を直接解析する。


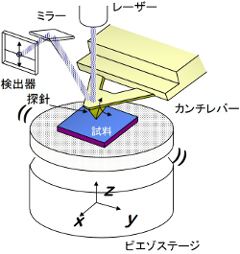
原子間力顕微鏡(AFM)に関する初期の研究は、測定の分解能や安定性の向上、および探針と表面間の相互作用に関する基本的な研究が多かった。しかしながら、現在では、下の左図に示されるような様々な分野の応用技術の解析手段として用いられる。ここでは、まず、右図のAFMの装置構成について説明する。AFMは、次の三つの要素から構成されている。(ⅰ)ナノメーターの精度で試料位置を三次元に移動できるピエゾ素子、(ⅱ)試料表面の相互作用力を検出するカンチレバーおよび探針、(ⅲ)カンチレバーのたわみ量を検出するレーザー光学系。ここで、カンチレバーにはSi3N4膜などが多く用いられ、その長さは200μm、厚さは20μm程度である。その先端には、長さ20μmで先端曲率半径25nmのピラミダル型の微細探針がマウントされている。探針の先端角は69°である。これらの探針先端のSEM写真を下の右図に示す。
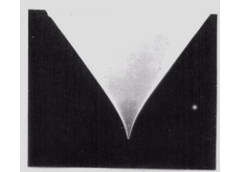
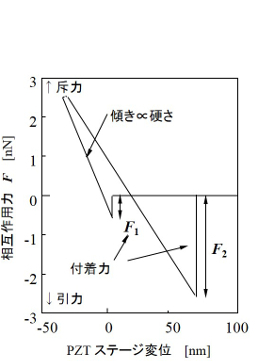
AFMによる付着力測定の基本となるフォースカーブについて説明する。下の左図はフォースカーブの一例を示している。これは横軸にピエゾステージの移動距離をとり、縦軸にレバーのたわみから換算した力(引力と斥力)を示している。ここで、カンチレバーが試料側にたわんでいる場合を引力とし、逆に反る場合を斥力として定義する。今、試料が探針から十分に離れている場合、レバーのたわみはゼロである。その後、ステージが上昇して探針に試料表面が近づくと、探針は試料表面に引き込まれて接触する。この時の力F1(N)をjump-in力と呼ぶ。さらにステージが上昇すると、カンチレバーは水平位置を過ぎて、上向きに反ることになる。実際の固体表面形状の観察は、この状態で行われることが多い。このとき、0.1N/m程度のばね定数を有するカンチレバーで表面測定をした場合は、試料表面を傷つけることなく測定することが可能である。その後、再びステージを下げると、水平位置を過ぎても探針は試料表面に吸着したままとなる。そして、最大の吸着力を示した後に、探針は試料表面から離れることになる。これが一連のカンチレバーの動作となる。光学系により測定したカンチレバーの撓みとばね定数から、探針の最大の吸着力F2(N)を求めることができる。この最大の吸着力は、一般に、pull-off力、あるいは、jump-out力ともいわれているが、二物体間に働くファンデルワールス(vdW, van der Waals)相互作用における引力の最大値に相当する。vdW力はあらゆる物質の表面間に働く電子雲の重なりを伴わない相互作用力であり、一組の電気双極子間に作用する。よって、電気双極子モーメントを生じるあらゆる物質間、原子間およびプラズマ間に対して、基本的に作用する力である。AFMの探針と試料間のvdW相互作用においても、同様なメカニズムが成り立つ。微小凝集体のvdW力の測定として、Larsonらのように,直径10μm程度の球状粒子をカンチレバーに取り付け,溶液中での粒子の付着挙動をDLVO (Derjaguin-Landau-Verwey-Overbeek) 理論を用いて解析した報告も多くされている。
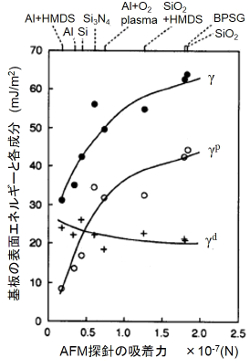
AFM探針の吸着力と固体の表面自由エネルギーとの相関について考察する。上の右図は接触角法で測定した各薄膜の表面自由エネルギーの分散および極性成分と、AFMで測定した探針の吸着力との関係を示したものである。吸着力Fは極性成分γpに強い相関を示し、分散成分γdにはあまり感度を有さないことがわかる。結果として、各成分の和である表面自由エネルギーγは、吸着力Fに正の相関を示すことになる。これは、探針の材質であるSi3N4の極性成分γpが分散成分γdに比べ高いため、固体表面の極性成分γpの変化に敏感に対応したものと考えられる。よって、AFM探針を用いることにより、固体表面の極性および分散成分などの相互作用の解析が可能になる。
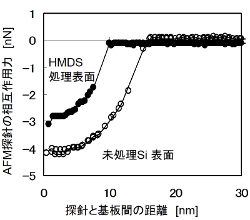
疎水化Si表面での相互作用
単分子層を形成するHMDS(ヘキサメチルジシラザン)処理による表面に対して相互作用力を解析する。この疎水化表面は、純水の接触角で100度程度を示す。また、酸素プラズマ処理を施したSi基板も用いる。この処理は、純水の接触角が0度を示す極端な親水化表面となる。これらの基板を用いて、AFM探針と疎水化・親水化表面との相互作用を解析できる。右図は、AFM探針の相互作用力の測定結果を示している。レナード・ジョーンズポテンシャルカーブに基づき、互いの距離が短くなるにつれて、相互作用力が変化している。また、相互作用曲線において、疎水化および親水化処理の影響が顕著に現われており、各固体の表面エネルギーの相互作用として定量解析できる。表面エネルギーγは分散成分γdと極性成分γpとの和として表すことができる。そして、相互作用エネルギーWは、以下の式のような各成分の二乗平均の和で表される。
![]()
ここで、HMDS単分子膜による疎水化処理は、γdを増加させる効果があり、酸素プラズマによる親水化処理はγpを増加させる効果がある。これらをもとに、得られた相互作用をまとめると下図のようになる。極性成分の高いSi製探針は、極性の高い酸素プラズマ処理面との相互作用が高く、分散成分の高いAu探針は、HMDS処理による疎水化表面と強い相互作用を有する。
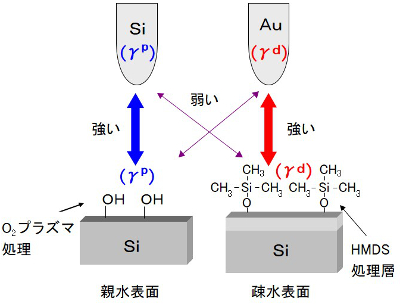
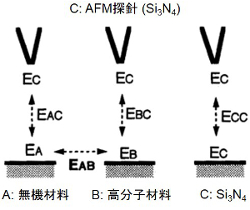
固体間の付着強度を非破壊的に推定することは、研究および産業上有用である。ここではAFM探針と固体表面との相互作用を利用して、未知の表面間の付着強度を推定する。右図において、薄膜Aと薄膜B間の未知の付着力を推定する。ここで薄膜Cは、探針材料であるSi3N4薄膜である。AFM探針と三種類の薄膜間の相互作用を、それぞれEAC、EBC、ECCで表す。これらの値は、フォースカーブ測定により求められる探針の吸着力(pull-off力)に相当する。また、相互作用に寄与する各薄膜表面の因子を、それぞれEA、EB、ECとする。これらは、測定不可能な物理量である。ここで、これらのパラメータ間の関係を下式で表す。
![]()
よって、薄膜Aと薄膜B間の相互作用エネルギーEABは、下式で表される。
![]()
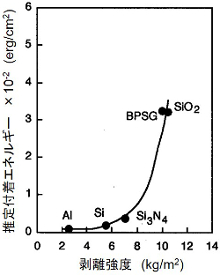
これにより、AFM探針により各表面での吸着力を測定し、EAC、EBC、ECCを求めることで、固体表面間の相互作用因子EABを計算で求めることができる。右図には上式で求めた相互作用エネルギー(推定付着エネルギー)と、引っ張り試験によるレジストと各薄膜間の接着強度との相関を示している。これら二つの物理量には正の相関がある事から、AFMにより未知の表面間の接着力を推定できる。
ここでは、付着現象に関わる相互作用力について、原子間力顕微鏡(AFM)を用いた解析を中心に解説した。表面処理や材質に依存した表面間の相互作用力を実測できることを示すとともに、これらを用いて、未知の表面間の付着力の推定が可能となる。このように、付着に関わる要因を直接測定することで、さらなる高品位な付着制御性が拡大する。
参考文献
- Akira Kawai, "Characterization of Surface Energetic Behavior by Atomic Force Microscopy", Jpn. J. Appl. Phys. 31, L977-L979 (1992).
- Akira Kawai, "Measurement Method of Adhesion Strength between Inorganic Materials and Polymer by Using Atomic Force Microscopy", J. Ceramic Society of Japan, 102, 1102~1104 (1994).
- 河合 晃, "原子間力顕微鏡により検出した薄膜の表面力と表面自由エネルギー成分との相関”, 日本接着学会誌, 31, 237-240 (1995).
- 河合 晃, "原子間力顕微鏡(AFM)を用いた微細探針走査法によるフォトレジスト微細パターンの接着性解析", 日本接着学会誌, 36, 2-9 (2000).
- Akira Kawai, "Direct Measurement of Resist Pattern Adhesion on the Surface with Silane-coupling Treatment by Atomic Force Microscope (AFM)", J. Photopolymer Science and Technology, 14, 513-518 (2001).
- Akira Kawai, "haracterization of SiO2 surface treated by HMDS vapor and O2 plasma with AFM tip", J. Photopolymer Sci. Technol, 16, 665-668 (2003).
水素結合成分による高分子膜の相互作用解析
塗膜の表面エネルギーは、付着、濡れ、被覆性などの重要な性質に強く関与する物理量である。通常、固体の表面エネルギーの2成分として、分散と極性成分を用いて解析する場合が多い。ここでは、極性成分の中の水素結合成分を分割して3成分として解析する。よって、付着エネルギーWaは次式のように表す事ができる。
![]()
![]()
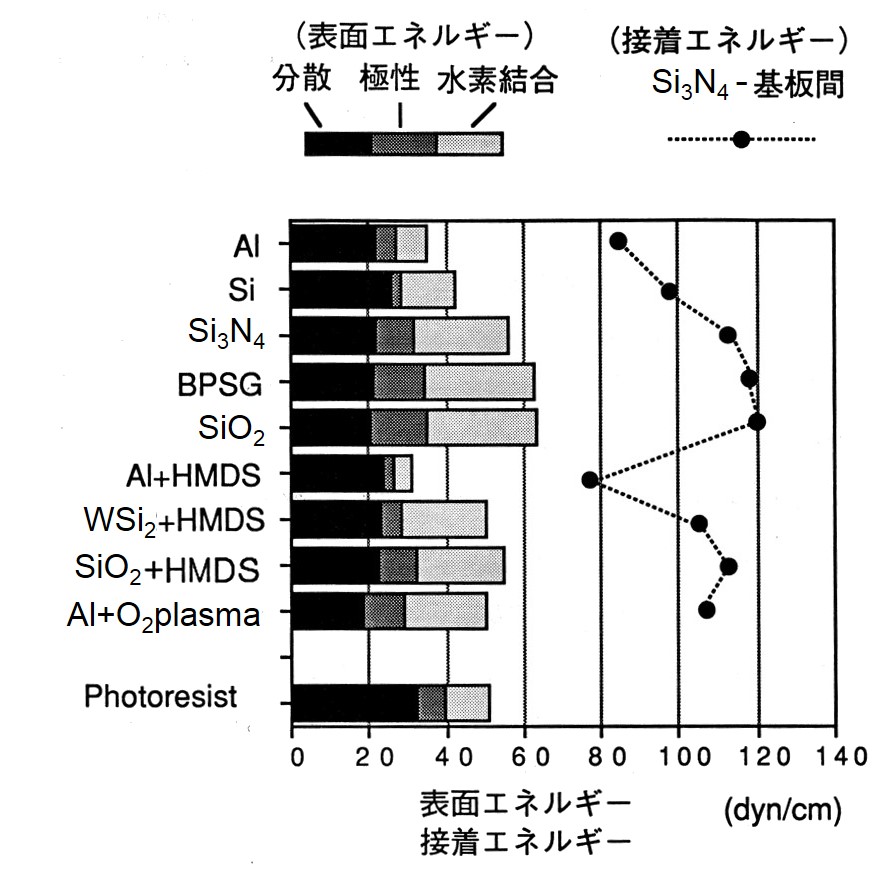
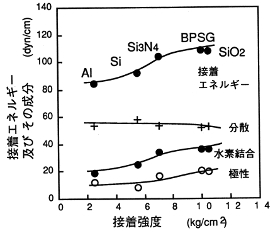
ここで添字d,p,hは、それぞれ、分散(非極性)、極性、及び水素結合成分を表している。これらは、γd,γp,γhの値が分かっている標準液を用いて各表面のエネルギー成分を求める事ができる。下の左図は接触角法で求めた無機基板表面の表面エネルギーの各成分、表面エネルギー、及びSi3N4探針に対する接着エネルギーを示している。分散成分は各基板間で大きい差はなく、約20mJ/m2の値となっている。又、有機物であるフォトレジストは大きい分散値を示している。極性成分は3成分の中で一番低い値を示しているが、各基板間の有意差が現れている。特にSi、Al又はHMDS処理をした基板では低い値を示し、SiO2, BPSG, Si3N4等の極性基板は比較的高い値となっている。水素結合成分は各基板間の有意差が一番大きい成分であり、その傾向は極性成分と似ているが値は大きい。固体の表面エネルギーはその極性、水素結合成分によって有意差が生じるが、分散成分には依存しない事がわかる。また、探針と表面間の接着エネルギーに関しても同様の事が成り立ち、接着エネルギーの有意差は主に極性と水素結合成分による事ことがわかる。
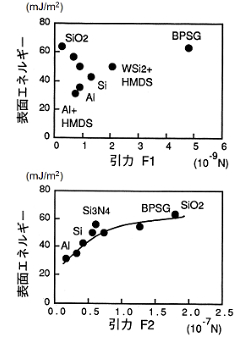
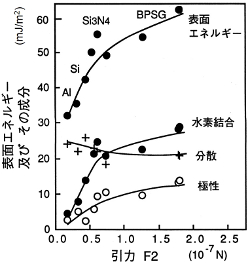
上の右図はAFMによる2つの表面力F1,F2と表面エネルギーとの相関を示している。探針が表面に近づく際に生じる引力F2と表面エネルギーには正の相関がみられている。高い表面エネルギーを有するBPSGやSiO2などは大きい引力値F2を示し、低い表面エネルギーを有するAlやSiに対しては低い引力を示す。すなわち、熱力学的な表面エネルギーは二物体が接触した際のエネルギー的平衡を主体としているため、二物体が離れている時の相互作用を表すものではない。よって二物体が離れている際の相互作用であるF1とは相関を示さないことが説明できる。又、引力F2はF1に比べ約100倍高い値を示している。また、引力F2が0の時に、表面自由エネルギーは約25mJ/m2の有限の値を示しているのがわかる。これより、表面エネルギーのある成分が探針と相互作用をしていないと考えられる。以上のように、探針によるプローブ法を用いる事によって、固体の表面エネルギーの検出が可能となる。右図には引力F2と表面エネルギーの各成分値との相関をしめしている。図より極性成分と水素結合成分は引力F2と正の相関を示す事がわかる。また、分散成分は引力F2に対し相関を持たず、よって上の右図のF2の引力値0の時の表面エネルギー25mJ/m2は基板の分散成分によるものであることがわかる。よって、探針プローブ法によって表面の極性及び水素結合の情報を得る事が可能である。ここで探針が固体表面間の引力より受ける弾性ポテンシャルエネルギー(すなわちカンチレバーの歪みエネルギー)を見積もる。歪みエネルギーEeは次式の様に表すことができる。
![]()
![]()
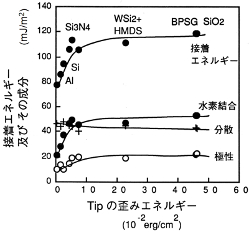
ここで、σは引力により探針が受けるストレス、EはSi3N4探針のヤング率(2.94×1011N/m2)、dはカンチレバーの膜厚(1μm)、Fは表面力の測定値(N)、kはカンチレバーのバネ定数(0.12N/m)、l(エル)はカンチレバーの長さ(200μm)を示す。下の左図には引力F2によって探針がうける歪みエネルギーEeと熱力学的な接着エネルギーとの相関を示している。両エネルギー間には正の相関がみられ、よって探針プローブ方式を用いて実際の接着現象を検出できる可能性が得られる。表面エネルギーの場合と同様、接着エネルギーの分散成分には相関が見られないが、極性と水素結合成分に対し相関が見られる。下の右図には接着強度と接着エネルギー成分との相関を示している。これらの間は、同様に、分散成分には殆ど依存しない事がわかる。接着エネルギーと接着強度は正の相関を示すが、分散成分によるバイアスが存在しているため、検出感度が低くなっている。
参考文献
- Akira Kawai, "Characterization of SiO2 surface treated by HMDS vapor and O2 plasma with AFM tip", J. Photopolymer Sci. Technol, 16, 665-668 (2003).
AFMによる高感度湿度センサー
両面を異なる材質で構成した微細カンチレバーを大気中に暴露した場合、湿度変化に応じて微細カンチレバーにたわみ変位が生じる。Au膜とSi3N4膜を微細カンチレバーの上下面に形成した場合、相対湿度の増加に伴ってレバーはSi3N4膜側へたわんだ。また、カンチレバーの両面をAu膜で形成した場合は、たわみ変位は殆ど生じなかった。すなわち、微細カンチレバーのたわみ変位は、レバーの上下面への水蒸気の吸着特性に対して差動的に生じると考えられる。これらのメカニズムを、固体表面での水蒸気のクラスター核生成における活性化エネルギーの点から考察した。微細カンチレバーのたわみ変位を利用することにより、湿度センサーとしての応用が期待できる。
固体表面へのガスや水蒸気などの吸着挙動は、接着、クリーンネス制御、センサー、触媒反応などのメカニズム解析において基本となる要素である。特に、水蒸気の吸着制御は、接着剤の塗布・乾燥処理や耐久性改善において重要な制御項目の一つである。従来から、湿度検出には、毛髪の伸縮を利用したものから、機能性セラミックスを利用した容量変化型などのさまざまな方式がある。近年、マイクロマシン技術の発展に伴い、微細カンチレバーを用いた機能性センサーが注目されている。これらは、アルコールや有機溶剤などのガスセンサーの確立を目的としている。そこで、ここでは、水蒸気吸着に伴う微細カンチレバーのたわみ特性に注目し、湿度センサーとしての可能性を考察する。

右図には、測定に用いた微細カンチレバー(オリンパス(株)、OMCL-TR400PA-1)のSEM写真を示す。微細カンチレバーの材質はSi3N4であり、光リソグラフィ技術で作製している。このSi3N4膜は、SiH2Cl2とNH3の混合ガスを用いた減圧CVD(Chemical vapor deposition)法により作製した。微細カンチレバーはV字形をしており、台座までの高さは100μm、一辺の幅は13.4μm、厚さは10μmである。また、微細カンチレバーのたわみ(deflection)とねじれ(torsion)方向のばね定数は、それぞれ0.089N/mと84N/mである。すなわち、この微細カンチレバーは、たわみやすく、ねじれにくい性質であることが分かる。よって、微細カンチレバーのたわみ変位だけを精度高く検出するのに適している。
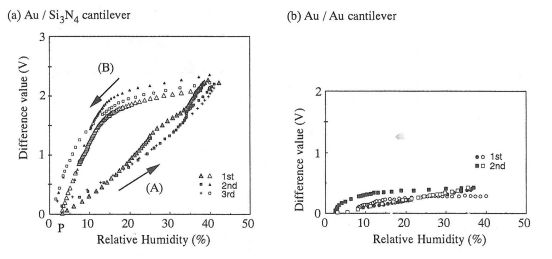
上図2a,2bには、チャンバー内の湿度変化に対する微細カンチレバーのたわみ変位(電圧表示)、及びヒステリシス特性を示している。ここで、たわみ変位の正の値は、水平に置かれた微細カンチレバーが下側にたわんでいることを示している。まず、チャンバー内を十分乾燥させて4%RHに達した時を測定開始点(P点)とした。次いで、相対湿度を40%RHまで徐々に増加させた。そして、加湿・乾燥サイクルを連続で数回行ってたわみ変位を測定した。上図2aのように、Au/Si3N4の微細カンチレバーでは、湿度増加に伴って下面のSi3N4膜側へたわむことがわかる(図中(A))。また、ヒステリシスは、反時計方向に存在しているのがわかる。特に、乾燥時(B)は、微細カンチレバーのたわみ変位の減少量が、加湿時(A)に比べて少ないことがわかる。これは、微細カンチレバー表面に存在する微細な凹凸形状により水蒸気の毛管凝縮が生じたため、乾燥時に水蒸気が脱離しにくくなったことが原因として考えられる。特に、微細カンチレバー下面のSi3N4膜表面において毛管凝縮が顕著であると考えられる。このような固体表面での脱着過程におけるヒステリシス現象は、BET(Brunauer, Emmett, Teller) 法などによるヒステリシス等温線においても報告されている。一方、上図2bのように、Au/Auで構成された微細カンチレバーの場合は、Au/Si3N4レバーに比べて、たわみ変位とヒステリシスが少ないことがわかる。よって、以上のことから、異なる材質で構成した微細カンチレバーを用いた場合、各膜の水蒸気に対する吸着特性の差が、たわみ変位として現われたことがわかる。
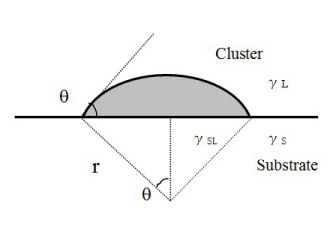
ここで、Si3N4膜とAu膜における水蒸気の吸着特性に着目して、微細カンチレバーに生じるたわみ変位のメカニズムを考察する。一般に固体表面へのガス分子の吸着及び脱離特性は、クラスター核生成モデルとして解析できる。まず、右図にあるように、平面基板上に吸着した表面エネルギーがγLである微小クラスター核の曲率半径をr、基板との接触角をθとする。ガス分子の吸着および脱離に伴うクラスター核生成の活性化エネルギーGは、熱力学的には以下のように定義される。
![]()
ここで、gvはクラスター核の凝集エネルギーである。また、f(θ)は生成核の形状パラメータであり、以下のように定義される。
![]() (4)
(4)
![]()
成分(mJ/m2)
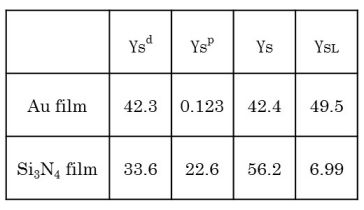
ここで、γSLはクラスター核(微小液滴)と基板間の界面エネルギーである。ここで、クラスター核の成長過程における基板材質の違いは、(4)式の形状パラメータf(θ)に反映される。そこで、クラスター核の形状パラメータf(θ)を見積もる。右表には接触角法で求めたSi3N4膜、Au膜の表面エネルギーと成分値を示している。また、水蒸気のクラスター核と基板との界面エネルギーγSLは、以下の式を用いて計算する。但し、水蒸気のクラスター核の表面エネルギーと成分には、前述の純水の値を用いた。γSLの計算結果は、右表にまとめている。
![]()
計算の結果、水蒸気の吸着を考えた場合、Si3N4膜およびAu膜上でのクラスター核生成の活性化エネルギー比(G SiN, /GAu)は、以下のように求められた。
![]()
すなわち、Si3N4膜上でのクラスター核生成の活性化エネルギーは、Au膜上に比べて約1/10であることがわかる。よって、水蒸気のクラスター核の生成および消滅は、Si3N4膜の方がAu膜よりも容易であることが推測できる。
以上の活性化エネルギーの考察から、右図にあるように、水蒸気の吸着及び脱離に伴う微細カンチレバーのたわみ変位のメカニズムを考察する。ここで、Si3N4膜上の吸着量をΔx、Au膜上の吸着量をΔyとすると、前述の微細カンチレバーの変位Δzは、次式で表される。
Δz=k(Δx-Δy)
ここで、kは比例定数であり、各膜のばね定数の関数として表される。加湿過程における微細カンチレバーのたわみ変位は、クラスター核が成長し結合することにより、連続膜を形成した時に生じた張力が原因であると考えられる。ここでは、水蒸気のクラスター核の成長がSi3N4膜上で顕著であることから、上式の(Δx-Δy)の値が増大し、微細カンチレバーはSi3N4膜側にたわんだものと考えられる。また、乾燥過程においても、Si3N4膜上での水蒸気膜の細分化と脱離が顕著に生じ、Au膜よりも早くクラスター核が消滅したと考えられる。しかしながら、前述の毛管凝縮の作用により、加湿と乾燥サイクル間においてヒステリシスが生じると考えられる。
以上のように、この微細カンチレバー型センサーは、異なる材質間の表面活性度の差、あるいは、反応速度の差などをリアルタイムで検出できる差動型センサーとして機能することがわかる。また、カンチレバーの片方の材質を固定すれば、ガス吸着センサーとして定量的な測定が可能になると考えられる。また、吸着媒体として、貴金属から高分子膜などの幅広い材料が利用できるため、さまざまなガス吸着に対応できると考えられる。しかしながら、微細カンチレバー型センサーには、図2aのようなヒステリシス低減の課題がある。解決策としては、レバー表面で生じる毛管凝縮を抑制するために、表面凹凸の少ない膜を形成するか、エピタキシャル成長技術により単結晶膜を形成することなどが有効である。また、センサーとしての高感度化には、微細カンチレバーのサイズをさらに小さくして、ばね定数を下げることが有効である。現在では、ばね定数が0.02N/mの微細カンチレバーが市販されている。また、他の分野への応用として、微細カンチレバー型センサーを真空中で動作させると、残留ガスの吸着を利用した熱源を有さない真空ゲージとしての作用が期待できる。今後、微細カンチレバーの高機能化に伴い、適用範囲が広がるものと考えられる。
固体表面でのAFM探針の吸着力解析
原子間力顕微鏡(AFM)を用いることにより、固体表面間の相互作用力の直接測定が可能になる。しかし、原子レベルで平坦な基板はマイカやグラファイトのへき開などでしか得られず、殆どの固体表面は表面粗さ(Rms)に代表されるような微小な凹凸を有している。また、通常の大気中では水蒸気が固体表面に吸着しており、AFMの探針と基板間にメニスカスが形成されてラプラス力が働くようになる。一般に、球/平面間の吸着式としては、F=4πRγで表わされるDerjaguin近似が代表的である。ここでは、薄膜の表面粗さ(Rms)を0.25~12.8nmの範囲、γを40~69mJ/m2、相対湿度を4%と40%に変化させて、微細探針の吸着力に及ぼす各要因の影響を考察した。その結果、これらの範囲においては、薄膜の表面粗さが吸着力測定に最も影響することが分かった。AFMを用いて固体表面の吸着力測定を精度高く行うためには、固体の表面粗さを少なくとも3nm程度に抑えること、あるいは表面粗さ効果を補正することが重要になる。
固体表面の吸着力測定は、固体間の接着と剥離、あるいは微粒子などの分散凝集制御において重要な知見を与える。1986年のBinnigらによる原子間力顕微鏡(AFM)の開発以来、固体表面間に働く相互作用力の直接測定の研究が盛んになった。しかしながら、固体表面間の相互作用に寄与する要因は多く存在するとともに、これらが同時に関与するために相互作用の要因分析がかなり困難となる。また、一般的に、マイカなどのへき開面やLB膜などの分子レベルで平坦な表面を除けば、通常の固体表面には多くの凹凸が存在している。その他、吸着水、帯電、有機汚染などの不確定要因は数多く存在する。それに反して、実用面では、大気中での表面制御技術の重要性は高まる一方である。河合研究室ではこれまでに、AFMを用いて様々な試料表面間の相互作用力を測定してきた。また、近年では、近接場光を検出原理として相互作用解析を行うなどの高機能型走査型プローブ顕微鏡を用いた研究例も増えてきた。しかし、試料の表面粗さなどの要因は、これらプローブ顕微鏡測定において共通に影響する要因であると言える
一般に、平坦試料上の半径Rの球に働く力Fは、Durjaguin近似として以下のように表わされる。
F=4πRγ
ここで、γは球および平坦試料の表面エネルギーを表わす。また、AFMの探針先端を半径Rの球で近似した場合、探針の表面エネルギーが平坦試料と異なる場合には、Burnhamの示した下式で表わされる。
![]() (2)
(2)
ここでγt、γsは探針および固体試料の表面エネルギーをそれぞれ表わす。一方、通常の大気中においては、探針および平坦試料表面に存在する吸着水によりメニスカスが形成されて、強いラプラス力が働くと予想される。毛管凝縮に基づくラプラス力は、一般的に下式で表わされる。
F=4πRγcosθ (3)
ここで、θはメ二スカスの接触角である。メニスカスの接触角は、大気中の相対蒸気圧(p/p0:相対湿度)に主に支配される。ここでは、以上の式において、表面エネルギー(γ)、表面粗さ(Rms)、相対湿度(p/p0)を変化させた場合、探針と試料表面間に働く力FをAFMを用いて直接測定する。

吸着力測定には、AFM探針と試料表面が常に接触するコンタクトモードを使用した。使用した探針の材質はSi3N4とAuの2種類である。探針形状はピラミダル型をしており、その長さは20μmである。また、先端曲率半径は25nmであり、探針の先端角は69°である。探針は、長さ200μmのカンチレバーの先端に取り付けられている。カンチレバーのばね定数は、0.098N/mである。使用した探針先端の電子顕微鏡(SEM)写真を右図に示す。探針の吸着力測定は、次の(1)~(3)の手順により行う。(1):探針を試料表面に低荷重(0.01nN)で吸着させる。この時、試料表面の変形は殆ど生じていない。(2):試料を下降させる。このとき、探針は相互作用により試料表面に吸着したままである。(3):探針が試料表面から離れた瞬間のそり量とカンチレバーのばね定数から、探針の吸着力を求める。
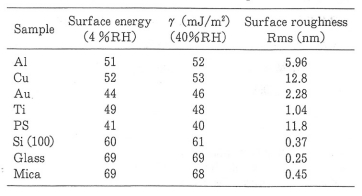
右の表1には、各試料の表面エネルギーおよび表面粗さの測定結果を示している。表面エネルギーは、40~69mJ/m2の範囲で変化している。また、前述のように大気中の湿度を4%および40%に変化させた場合、Au膜表面での吸着水膜厚は僅かながら増加している。しかしながら、表面エネルギーはそれほど大きく変化していない。通常、吸着水による固体の表面エネルギー変化は、拡張圧πeとして下式で表わされる。
γs=γsv-πe
ここで、γsvは飽和蒸気圧下での固体の表面エネルギーを意味する。ここでの湿度変化範囲においては、各基板において0.1~2mJ/m2程度の変化であることが表1から分かる。

上の図2はAFMで測定した各試料の表面形状を示している。蒸着過程における粒成長の違いにより、表面形状が異なっている。特に、凝集性の比較的高いAl膜やCu膜などは、結晶粒が比較的大きいことが分かる。一方、凝集性の低いAu膜などは、結晶粒は小さく平坦な表面を形成していることが分かる。AFMで測定した各試料の表面粗さは、表1にあるように、0.25~12.8nmの範囲で変化していることが分かる。次に、これらの試料表面の吸着力測定結果について述べる。
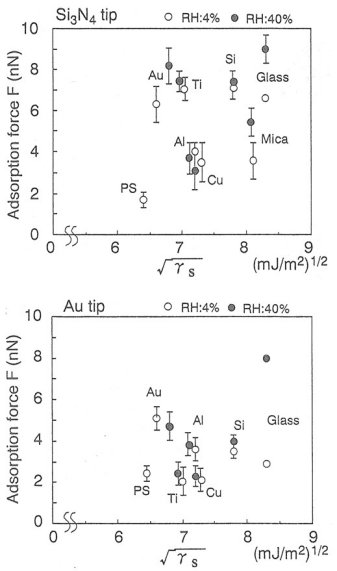
上の図3は各試料表面におけるAFM探針の吸着力と、試料の表面エネルギー(平方根)との関係を示している。その結果、探針の違いおよび湿度変化に対してBurnhamらが提示した(2)式に基づく相関は示さないことが分かる。Burnhamらの実験は、乾燥窒素中で、マイカ及び熱酸化膜上の単分子膜といった分子レベルで平坦な基板を用いて解析している。よって、各試料表面間の粗さの差が顕著である場合は、吸着力解析に悪影響を及ぼすと考えられる。そこで、試料の表面粗さと探針の吸着力との相関を考察する。
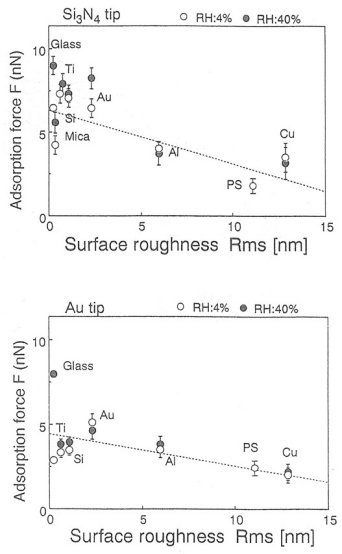
上の図4はAFM探針の吸着力と試料の表面粗さとの関係を示している。探針の材質、および、湿度の差などの測定条件の変化にも拘わらず、探針の吸着力は試料の表面粗さに相関を示すことが明確に分かる。よって、AFM探針の吸着力の測定結果は、大気中の湿度変化、および試料の表面エネルギーの違いよりも試料の表面粗さに主に支配されることが分かる。本研究の場合においては、試料の表面粗さを少なくとも3nm以下にすることが望ましいと考えられる。
図3および図4のAFM探針と試料表面間の吸着力について、試料の表面粗さを考慮したモデルを構築して検討する。まず、(2)式において、試料表面の凹凸は、探針先端の曲率半径に比べて相対的に無視できるとしている。そこで、試料表面が平坦ではなく凹凸を有しており、これを曲率を有した球の集合体として近似する。すなわち、(2)式の曲率半径Rは、次式のように探針と試料表面の曲率半径、RtとRsの幾何平均として表わすことが出来る。
![]()
また、吸着水が存在する場合には(3)式を考慮する。
![]() (6)
(6)
この(6)式が、本研究における基本式になると考えられる。試料表面の有限の粗さを曲率半径Rsとして平均的に表わすのは容易ではないが、二乗平均粗さRmsの変化はRsが変化することに相当する。そこで、基板の表面粗さが吸着力に与える影響を考察する。
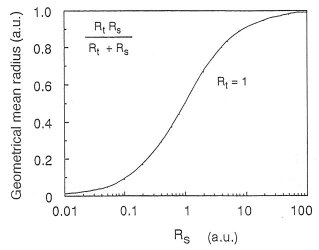
右図は規格化した幾何平均曲線を示している。試料表面の曲率半径Rsの減少に伴い、幾何平均半径は減少する。また、探針と試料表面との曲率半径が一致する時(Rt=Rs)は、規格化した幾何平均半径は0.5になる。実験に使用したAFM探針の曲率半径は、25nmであり、また、図2のAFM像から、試料表面の平均的な凹凸の曲率半径が約2nm~200nmの範囲で変化しているとすると、幾何平均値は1.8~22nmの範囲で変化していることになる。河合研究室は、既に、PSL球を用いて、探針の吸着力とPSL直径との相関が、この幾何平均則に従って変化することを確認した。すなわち、試料表面の凹凸によって、探針の吸着力の絶対値は大きく影響を受けることを示している。また、本実験においては、γsを40~69mJ/m2まで変化させるとともに、γtを51.4mJ/m2と56.3mJ/m2のものを用いているために、結局、![]() の値は45.3~62.3mJ/m2の範囲まで変化させたことになる。これらの値から考えると、試料の表面エネルギー変化が吸着力に影響しても妥当であると考えられる。しかし、実際には表面粗さが主に影響する結果となっている。この理由として、以下に挙げるような試料の表面凹凸が原因となる要因がさらに関与しており、吸着力に影響していることが考えられる。
の値は45.3~62.3mJ/m2の範囲まで変化させたことになる。これらの値から考えると、試料の表面エネルギー変化が吸着力に影響しても妥当であると考えられる。しかし、実際には表面粗さが主に影響する結果となっている。この理由として、以下に挙げるような試料の表面凹凸が原因となる要因がさらに関与しており、吸着力に影響していることが考えられる。
(1)探針と試料表面の接触に伴う変形と接触面積の変化。
(2)探針の接触点近くに存在する試料表面の突起による影響。
(3)試料表面の凹凸に起因する接触帯電や有機汚染分布などの不確定要素。
上記項目が定量化されれば、吸着力の解析精度はさらに高まるものと考えられる。
AFMを用いた一括破壊試験法
半導体素子製造プロセスに用いられる有機ドットパターンに原子間力顕微鏡(AFM)の探針から荷重を加えて破壊することで,パターンの付着力を直接に解析できる。今回,KrFエキシマレーザー対応化学増幅型レジスト(直径110~240nm)のパターン破壊荷重の度数分布の簡便な測定法を新たに提案し,その破壊挙動を解析する。ドットパターンの破壊荷重依存性には閾値が存在する。よって,閾値荷重及び初期不良パターン数からレジストパターンの付着信頼性を評価できる。AFMによるその場観察から,パターン破壊後の基板表面にはレジスト残渣が観察された。よって,パターン自身が凝集破壊していることがわかった。また,本手法をArFエキシマレーザー対応化学増幅型レジストにも適用して妥当性を確認した。そして,3次元の有限要素法により,加重時に発生するパターン内部の応力分布を解析した。これにより,応力集中がパターン破壊に大きく影響していることを明らかにした。
近年,オーディオ製品などのデジタル化に伴い,表示素子やメモリデバイスに代表される半導体素子の需要は急激に拡大している。これらの半導体素子では,製品の小型化,低消費電力化,及び記録密度の向上のために回路パターンの微細化が必要とされる。特に,メモリデバイスの回路パターン形成時には,エッチング用マスクとされる有機レジストパターンとして0.1μm程度の非常に微細な線幅が要求されている。現在,有機微細レジストパターンはKrFエキシマレーザーなどを用いた光リソグラフィにより形状を転写しており,リソグラフィ条件の最適化は光学シミュレーションに頼る部分が増大している。しかしながら,光学的には解像されている微細レジストパターンが,形状の転写後の現像プロセスにおいてリンス液(純水)のラプラス力により倒壊することが知られている。この倒壊現象の回避には,微細レジストパターンの付着力を定量解析し,光学シミュレーションや材料設計にフィードバックすることが必要とされる。しかし,サブミクロンオーダーの有機微細パターンの機械的物性や無機基板との接着性は直接に解析する手法が少なく,バルクの物性で代用することが多かった。一方で,原子間力顕微鏡(Atomic Force Microscope:AFM)の登場は,表面科学の分野における解析技術を飛躍的に向上させた。AFMは,原子レベルの空間分解能を有し,探針と試料表面の相互作用力を実測できる。また,探針により試料表面を加工する技術も一つの分野として確立しており,ナノメータースケールの加工技術として注目されている。そこで,我々はAFMの微細探針から荷重を加えて有機微細レジストパターンを直接に倒壊するといった付着挙動の解析技術を提案し,その妥当性を確認してきた。しかしながら,本手法はAFMの操作にある程度の熟練が必要であると共に,1個のパターンを選択して試験することから多数のパターンに対する評価が困難であった。したがって,パターンの破壊荷重を統計的に解析するのが容易でなかった。そこで,ここではKrFエキシマレーザー対応化学増幅型レジストのドットパターンに対して,破壊荷重の定量測定法を新たに提案する。この手法は,AFMによるパターン形状の観察を同時に行える簡便な操作であることを特徴としている。さらに,この技術をギガビットクラスのメモリデバイス用のマスク材料であるArFエキシマレーザー対応化学増幅型レジストに対して適用する。また,3次元の有限要素法(Three-Dimensional Finite Element Method; 3D-FEM)を用いてパターン内部の応力分布を解析する。これにより,パターンの破壊挙動(凝集破壊,界面破壊)と応力分布との相関を明らかにする。
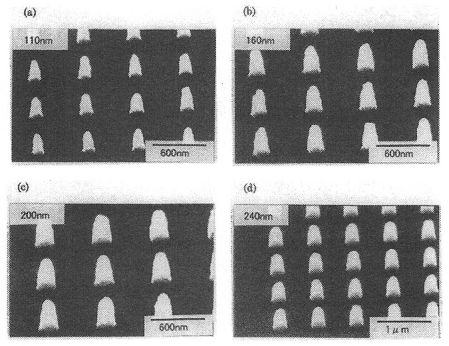
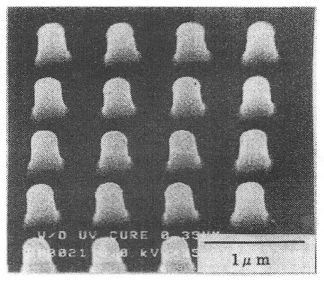
試料としてKrFエキシマレーザー(波長248nm)対応化学増幅型レジスト,及びArFエキシマレーザー(波長193nm)対応化学増幅型レジストを用いた。KrFエキシマレーザー対応化学増幅型レジストは,HMDS(Hexamethyldisilazane)によるシランカップリング処理を施したSi熱酸化膜(SiO2)上にスピンコート法により塗布した。HMDS処理は,60℃で45秒間行った。そして,ドット形状をレジスト膜に転写し,TMAH(Tetramethylammoniumhydroxide)2.38%水溶液で現像することでドットパターンを形成した。また,ドットパターンには電子線を照射することで表面の硬化処理を行った。上図に実験で用いた様々な寸法のドットパターンのSEM写真を示す。パターンの高さは593nmであり,各ドットパターンの直径は110nm,160nm,200nm,及び240nmであった。ArFエキシマレーザー対応化学増幅型レジストも同様に,HMDS処理(90℃,180秒)したSi熱酸化膜上に形成し,電子線照射による表面の硬化処理を施した。右図のSEM写真において,パターン高さは520nmであり,直径は335nmであった。
AFM装置としては,探針の荷重を常に一定にコントロールするコンタクトモードAFMを使用する。実験では,試料の帯電による観察像の歪みを除去するために,金コートを施したSi3N4製の探針(以下,AFM探針)を使用した。探針先端のSEM写真を下図に示す。AFM探針は,先端の曲率半径が25nmのピラミダル形状であり,これはカンチレバーの先端にマウントされている。カンチレバーは短冊型をしており,長さは100μm及び厚さは0.8μmである。また,幅は20μmと40μmの2種類を用いており,それぞれのカンチレバーのばね定数は0.37N/mと0.75N/mである。破壊荷重の測定においては,カンチレバーのばね定数をレジストパターンの付着力に対応させて選択することにより,広範囲の試料を測定することができる。実験において,付着力の比較的小さいKrFエキシマレーザー対応化学増幅型レジストには,ばね定数0.37N/mのカンチレバーを用いた。また,付着力の比較的大きいArFエキシマレーザー対応化学増幅型レジストには,ばね定数0.75N/mのカンチレバーを用いた。

AFM探針を用いた簡便な破壊荷重の測定法を以下に提案する。
①:探針から試料表面に加える荷重を極力低くして,ドットパターンの形状を観察する。観察像から破壊試験に用いるドットパターンの数を決定する。適切な観察範囲を設定することにより,破壊試験に用いるパターンの数を任意に選択できる。これは,本手法の特徴の一つである。今回の試験では,探針の走査速度が4μm/sになるように,観察範囲を一定[4μm×4μm]に設定した。その結果として,直径が110nm及び160nmのドットパターンは25個を用いた。直径が200nmのドットパターンは20個を用い,240nmのドットパターンは16個を用いた。
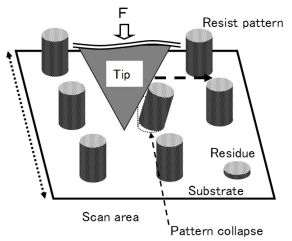
②:探針に荷重を加えながら選択したドットパターンを観察する。右図に観察中の探針とドットパターンとの位置関係を模式的に示す。ここで,荷重Fによりドットパターンの内部に生じた応力によって,パターンが破壊する。このときのパターンの破壊荷重はFとなる。この値は,ドットパターンの付着力に相関がある。
③:破壊したパターン数を計測する。ドットパターン形状の観察中に破壊が生じた場合,そのパターンの存在した位置には,残渣もしくは基板表面が観察される。よって,ドットパターンを破壊するためのAFM観察と同時に,破壊したパターン数の計測を行う。
④:荷重をさらに増加してから②,③を繰り返すことで,破壊パターン数の破壊荷重依存性を測定する。
⑤:全てのドットパターンが破壊した後,基板上に残る残渣の有無及び形状を観察して,破壊挙動を解析する。
このように,本手法は形状観察を行う同時に,AFM探針の荷重を変化させることにより微細パターンの破壊荷重を同時に測定できるといった簡便な操作であるといえる。
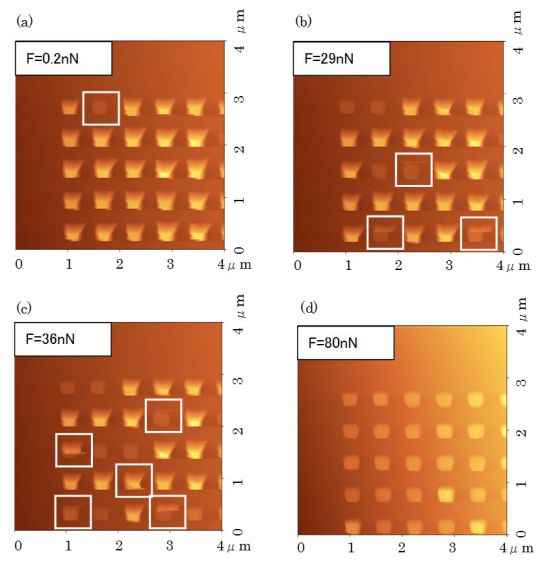
上図(a)~(d)は,本手法による破壊荷重測定を行った代表的なAFM像である。試料は,直径が110nmのKrFエキシマレーザー対応化学増幅型レジストのドットパターンである。上図(a)は,探針の荷重が0.2nNの低荷重で観察したAFM像である。この試料では,既に低荷重でパターンの破壊が生じている(図中の白枠部分)。さらに荷重を29nN,36nNに設定して観察したAFM像がそれぞれ,上図(b)及び(c)である。荷重が29nNにおいて3個のパターンが破壊している。そして,荷重を36nNに増加すると5個のパターンが破壊している。上図(d)は荷重を80nNまで増加して全てのパターンを破壊した後に,基板表面に残った残渣の観察像である。これより,直径が110nmのパターンの破壊は,すべて凝集破壊により生じたといえる。
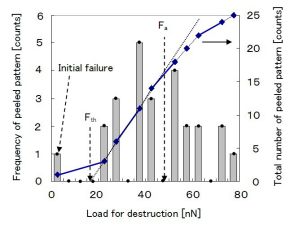
右図は,横軸にパターンの破壊荷重をとり,縦軸に破壊したパターンの度数(ヒストグラム)及び累計(実線)を示したグラフである。このように本手法によれば,レジストパターンの破壊荷重を度数分布として測定できる。破壊パターンの度数を示すヒストグラムの1本は,AFMによる1回の像観察中に生じたパターン破壊数に相当する。よって,右図の全測定は16回のAFM観察により得られている。破壊パターンの累計は破壊荷重が20nN付近から直線的に増加している。そこで,累計曲線の立ち上がり部分に接線を引き,その接線とx軸との交点を閾値荷重Fthとして定義した。さらに,Fth以下の低荷重で破壊したパターンは,他のパターンと破壊要因が異なる可能性がある。そこで,これらは初期不良パターンとして区別した。
剥離数との関係
剥離数との関係
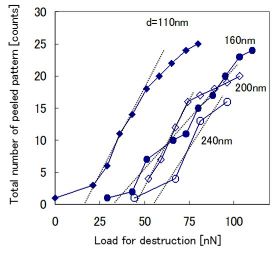
次に,本手法を用いて破壊荷重のパターン直径依存性を測定した。その結果を上の左図に図示する。ドットパターンの直径が太くなるに従って,破壊パターンの累計曲線は高荷重側にシフトしている。これより,パターンの破壊荷重は直径に依存して増加する傾向があることがわかる。そして,試験後の基板表面には全ての寸法のパターンに残渣が観察されていることから,破壊挙動は凝集破壊であることを確認した。
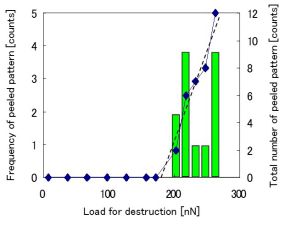
さらに,図2に示したように,ギガビットクラスのメモリデバイス対応のレジスト材料であるArFエキシマレーザー対応化学増幅型レジストの破壊荷重分布を測定した。その結果を上の右図に示す。閾値荷重Fthは,187nNであると測定された。また,破壊した12個のドットパターンのうち2個において残渣が確認されたが,その他のパターンは残渣が観察されなかった。つまり,このドットパターンの破壊では凝集破壊と界面破壊の両方が生じることがわかった。上の右図と左図から導出した閾値荷重Fth,破壊荷重の平均値Fa及び初期不良パターンの数Nをまとめたのが下表である。
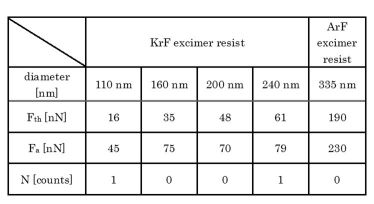
上表より,KrFレーザー対応化学増幅型レジストの閾値荷重Fthは,直径が太くなるに従って増加している。また、初期不良パターンは直径110nmおよび240nmにおいて1個ずつ見つかった。ここで,半導体素子製造プロセスの場合,半導体集積回路の中に回路の不良が1箇所でも存在すると動作しない。そのため,初期不良パターンを無くすことが,歩留りの向上に必要であると考える。また,リンス液(純水)のラプラス力に対するレジストパターンの安定性は閾値荷重Fthを高くすることで達成できると考えられる。
一方,破壊荷重の平均値Faは必ずしもパターンの直径に依存していない。これは,他の破壊要因が影響していると考えられる。そこで,図6において破壊パターンの累計曲線の立ち上がりに引いた接線(点線)を見ると,平均値Fa付近までは接線とよい一致をしているが高荷重側になるに従って接線からずれている。この部分は,AFM探針の走査回数の増加に伴うパターン疲労の影響が現れていると考えられる。結果で述べたように本手法では,全工程で16回程度の形状観察を行う。この回数は,探針と1個のパターンとが約1500回の接触することに相当する。高荷重側においては,荷重の増加と共に接触回数も増加し,パターンの疲労が多く生じることを確認している。したがって,パターンの疲労により分布図の高荷重側にばらつきが生じたと考えられる。反対に,低荷重側では疲労破壊が少ないといえる。このことからも,本手法で測定した破壊荷重分布に基づいてレジストパターンを評価する場合は,接触回数の多い高荷重領域を避けて,低荷重領域の閾値荷重Fthと初期不良パターン数Nで比較することが妥当であるといえる。
次に,図8のArFエキシマレーザー対応化学増幅型レジストの破壊荷重分布について考察する。破壊荷重は,図7のKrFエキシマレーザー対応化学増幅型レジストより大きくなっている。これは,ArFエキシマレーザー対応化学増幅型レジストの直径が335nmと太かったことが主な原因であると考える。ArFエキシマレーザー対応化学増幅型レジストのドットパターンの破壊要因として,凝集破壊と界面破壊の両方が混在した。そこで,これらの破壊要因をドットパターンの内部応力分布から考察する。
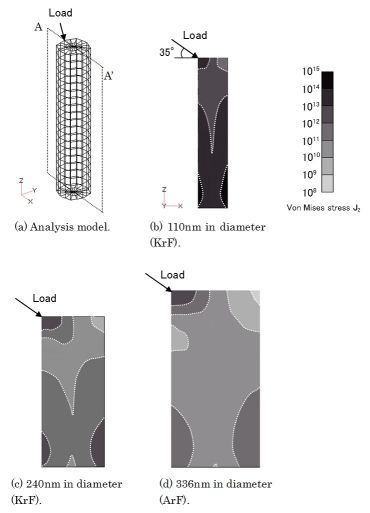
3D-FEMによりドットパターン内部の応力分布解析を行い,破壊試験後の残渣形状との相関を考察する。解析は3D-FEMソフト(PHOTO-ELASJW;PHOTON Corporation)を用いて弾性変形静解析により行う。材料の物性値は,代表的な高分子材料であるポリスチレンを参考にしてヤング率E=3GPa,ポアソン比ν=0.34を入力した。上図(a)に解析モデルのメッシュ形状を示す。要素の形状は4面体である。ドットパターンの形状は,近似的に八角柱とした。荷重は探針形状を考慮して,図中の矢印のようにモデルパターン上面の外周の1点から中心方向へ35度下向きに加えた。また,モデルの底面は基板界面との接着面であるため,不動点として固定した。応力は次式で与えられるVon Mises応力J2で表示している。
![]()
ここで,σは垂直応力,τはせん断応力である。
上図(b)から上図(d)は,各レジストパターン寸法に対応した解析結果を示す。これらの図はパターン内部の応力分布が見やすいように,荷重ベクトルに沿った断面A-A’で表している。上図(b)と上図(c)は直径110nm及び240nmのKrFエキシマレーザー対応化学増幅型レジストパターンにそれぞれ対応している。パターンの高さはいずれも590nmである。上図(d)は直径336nmのArFエキシマレーザー対応化学増幅型レジストに対応しており,パターンの高さは670nmである。
上図(b)~上図(d)より,パターンの内部応力は,底面から40nm~50nm上部に集中していることがわかる。特に直径が細いほどこの傾向は顕著に見られる。そこで,底面の応力と応力集中点の応力を比較する。上図(b)より,直径が110nmのパターンモデルは,応力集中点の応力が1.75×1014であり,底面の応力が1.11×1014であった。よって,応力集中点の応力は底面と比較して1.58倍になっていた。同様に上図(c)の直径が240nmのパターンでは1.33倍であり,上図(d)の直径が336nmのパターンでは1.24倍であった。つまり,パターンの直径が細くなるほど底面に比べて応力集中点の応力が大きくなるといえる。パターンの破壊が生じる位置は,レジストの凝集力と基板との接着力,及びその位置の集中応力のバランスによって支配される。その結果として,破壊挙動は凝集破壊と界面破壊に分かれると考えられる。上図(b)のように直径が細いことにより底面に比べて応力集中点の応力が大きい場合は,応力集中点から破壊が生じやすい。この場合は,凝集破壊に対応する。これに対し上図(c)のように底面と応力集中点の応力とが比較的近い場合,凝集力と接着力のバランスにより凝集破壊と界面破壊が選択的に生じるといえる。そのためにArFエキシマレーザー対応化学増幅型レジストのドットパターンは,両方の破壊が生じたと考えられる。以上のことから,パターンの直径が細くなるにしたがってレジスト材料の凝集力を向上させることが,付着力増加のために重要になることが考察できる。
AFMによる微粒子間の相互作用力解析
微細粒子の付着機構は,原子間力顕微鏡(AFM)の相互作用測定により解析できる。ポリスチレンラテックス(PSL)凝集粒子とAFM探針間に作用する相互作用力の粒径依存性を,乾燥大気中でのフォースカーブ測定により解析できる。粒径42nm~1μmの範囲で,相互作用力の粒径依存性は一般的なDMT理論より導かれる幾何平均の粒径依存性と異なる。相互作用に基づく粒子の変形と隣接しているPSL粒子の寄与の導入により,AFM探針とPSL凝集粒子間の相互作用の測定結果を説明できる。
微粒子の付着要因の一つであるvan der Waals(vdW)力は表面間に作用する相互作用力であり,表面物理,コロイド化学,生化学などの分野を中心に活発に研究が行われてきた。vdW力の理論的な研究には,Hamaker,Derjaguin,Lifshitzのものがある。その後,実験的研究が表面力測定装置(Surface Force Apparatus)などによって行われてきた。近年,原子間力顕微鏡(Atomic Force Microscope, AFM)を用いたvdW力に関する研究は,理論的,あるいは実験的に盛んに行われている。Larsonらのように,直径十μm程度の球状粒子をカンチレバーに取り付け,溶液中での粒子の付着挙動をDLVO (Derjaguin-Landau-Verwey-Overbeek) 理論を用いて解析した報告も多々なされている。また,ジャンプアウト時の付着力と試料の表面自由エネルギーの極性成分との間に,正の相関があることも知られている。
微粒子の付着および凝集挙動は,JKR (Johnson-Kendal-Roberts) 理論やDMT (Derjaguin-Muller-Toporov) 理論に基づき,表面自由エネルギーや弾性率などの物性値を用いて解析できる。しかしながら,膜厚数百nmの薄膜材料の弾性率は,形状効果によってバルクに対して変化すると考えられる。そのため,粒径数百nmの微粒子同士の付着挙動は,粒径数μmの微粒子やバルクの付着挙動と異なることが考えられる。また,Marquardtらは,直径10nm~10μmの金属微粒子の誘電関数がバルクに対して異なることを報告している。一方,微粒子間の相互作用力に関する研究も,近年活発になってきている。例えば,微粒子を主原料とするトナーインクや顔料などの技術分野においては,凝集性や付着挙動が重要になる。またULSI (Ultra-Large-Scale-Integration)プロセスにおいては,設計寸法は10nm以下に迫ってきている。ショート,断線等の歩留まり低下の原因となる付着微粒子のサイズの目安は,デザインルールの1/3程度と考えられる。この為,洗浄プロセスや微細加工プロセスなどにおいては,数nm以下の粒径の微粒子の付着力低減技術の確立が重要になると考えられる。以下,AFM探針先端を球近似し,フォースカーブを用いて,AFM探針と粒径42nm~1μmのポリスチレンラッテックス粒子(Polystyrene latex; PSL)の間に作用するジャンプアウト時の付着力とジャンプイン時の近距離引力の粒径依存性を解析した結果について考察する。DMT理論を基本に,PSL粒子の変形の効果及び隣接しているPSL粒子の相互作用の影響の点を考慮して粒子間の相互作用の理論式を補正し,粒子付着性を検証する。
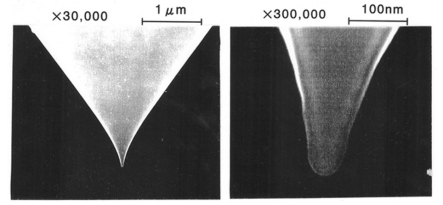
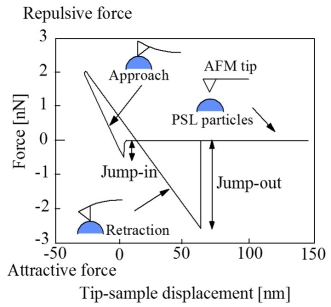
実験として,PSL粒子(日本合成ゴム,STADEXシリーズ)は,平均粒径42, 73, 100, 136, 206, 298, 1001nmのものを用いた。粒径の標準偏差は,それぞれ12.8, 4.79, 2.58, 2.83, 1.81, 1.53, 2.36%である。HF洗浄処理により自然酸化膜を除去したSi(100) waferに,これらPSL粒子の分散された電解液を滴下し,自然乾燥させたものをサンプルとした。バルクのサンプルとして,ポリスチレンシート(PS sheet : 三菱樹脂,ヒシプレート) を用いた。付着力と近距離引力は,AFM(セイコー電子工業(株)製,SPA-300)を用いて,右図に示すフォースカーブで求めた。付着力と近距離引力には,それぞれ右図中に示すジャンプアウトした時とジャンプインした時の力を用いた。カンチレバーにはサンプルの帯電の影響を除去するためAuコートされたSi3N4(オリンパス光学,OMCL-TR400PB-1,バネ定数0.1N/m)を用いた。上図に示すAFM探針のSEM観測の結果,先端曲率半径は40nmであった。吸着水によるラプラス力の影響を除去する為,測定は乾燥雰囲気中(4%RH,20℃)で行った。フォースカーブは,AFM表面像観察の後,AFM探針を任意のPSL粒子の頂点直上セットし測定を行った。付着力と近距離引力は,面内の各PSL粒子に対しランダムに20回行い,平均値及びその標準偏差で評価した。PSL粒子の弾性変形を,二次元有限要素法で解析した。ここでAFM探針とPSL粒子のヤング率はそれぞれ150GPa,2.7GPaとし,ポアソン比はそれぞれ0.24,0.34とした。
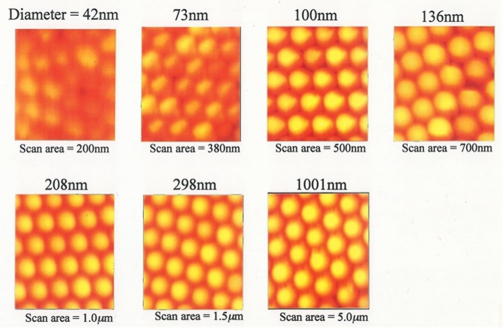
上図は各粒径におけるPSL凝集体のAFM像を示している。各PSL粒子は基板上で最密充填構造をとって凝集している。これらの粒子1個の中心位置において,AFM探針に働くジャンプアウト時の付着力とジャンプイン時の近距離引力を下の右図(a),(b) に示す。付着力と近距離引力は,粒径の減少に伴い減少することがわかる。
球状粒子間の相互作用力の粒径依存性は,DMT理論により幾何平均半径に比例することが知られている。
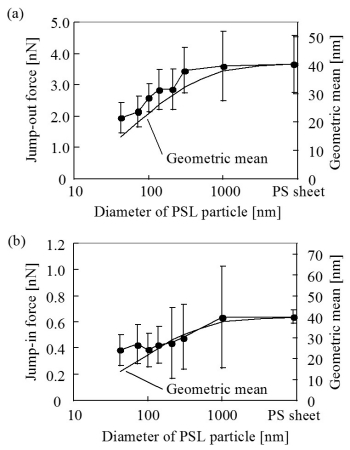
(a) ジャンプアウト力 (b) ジャンプイン力
![]() (1)
(1)
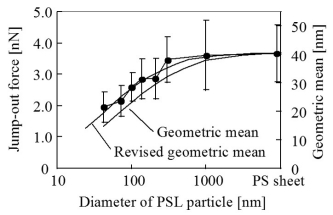
ここで,AはHamaker定数,D0はAFM探針とPSL粒子の最表面間距離,RTip,RPSLはAFM探針の曲率半径とPSL粒子の半径である。PSL粒子の半径,及びAFM探針の先端曲率半径は既知である。測定では同一のAFM探針を用い,サンプルには同一のポリスチレンを用いていることから,Hamaker定数Aを一定と仮定すると,測定系の相互作用力と近距離引力は幾何平均半径を用いて解析することができる。そこで,上式で表わされるvdW力との比較を行う為,右図 (a),(b)に幾何平均半径のPSL粒径依存性を示した。ジャンプアウト時の付着力は,どのPSL粒径についても,上式(RTipとRPSLから計算される幾何平均半径)と比べて大きくなっている。一方,ジャンプイン時の近距離引力は,粒径100nm以上のPSL粒子に対して上式と一致しているが,粒径100nm以下のPSL粒子に対してはジャンプイン時の近距離引力が大きくなっている。
右図(a)において,幾何平均半径の実験値と計算値が合わない原因は,AFM探針との接触によるPSL粒子の変形の寄与によるものと考えられる。そこで,PSL粒子の変形の付着力への効果に関して,以下の考察を行った。
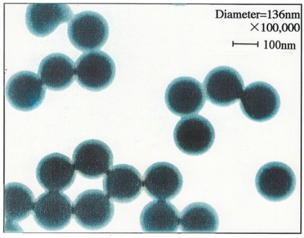
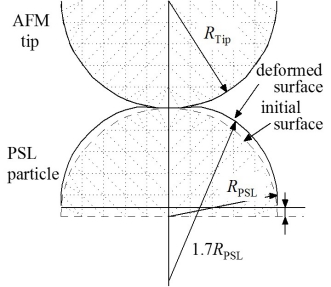
上の左図は,溶液中のPSL粒子のTEM像を示している。上の左図より明らかなように,PSL粒子間の接触面は大きく歪んでいる。これは,vdW引力に起因する付着力の作用で互いに吸着し,接触部でPSL粒子の表面が弾性変形を起こしたためと考えられる。そこでAFM探針との接触変形により変化したPSL粒子の曲率半径を補正する目的で,有限要素法解析によりシミュレーションを行った。シミュレーションした結果を上の右図に示す。ここで,PSL粒子の押し込まれる距離をTEM像と同程度と仮定し,シミュレーションではPSL粒子の半径の10%とした。これより,PSL粒子の歪みによる表面形状の変形が定量化できる。特に接触部付近において,PSL粒子表面の曲率半径は,変形前の半径の約1.7倍に達している。また,PSL粒子の曲率半径はAFM探針との接触点から離れるにつれて減少している。ここで接触変形によるPSL粒子の曲率半径をR*PSLとし,(1)式のPSL粒子の半径RPSLをR*PSLと置き換える。これより,補正後の相互作用力は下式のようになる。
![]()
図4 (a) のジャンプアウト時の付着力のPSL粒径依存性にフィッティングした結果,R*PSL≒1.7 RPSLが得られた。 R*PSLを用いて求めた幾何平均のPSL粒径依存性を右図に示す。これより,ジャンプアウト時の付着力は,AFM探針との接触により変形したPSL粒子の曲率半径の増加に依存していると考えられる。
ジャンプイン時の近距離引力には,AFM探針の接触によるPSL粒子の変形は影響しないと考えられる。しかし,図4 (b)にあるように, 粒径100nm以上のPSL粒子では,実測値は(1)式に従っているが,それより小さいPSL粒子との近距離引力は,(1)式より大きくなっている。そこで,隣接する周囲のPSL粒子の影響を考察する。
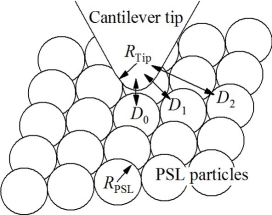
(1)式は,一対の球状粒子間に作用する相互作用力に関する記述である。実験で用いたPSL粒子は,図3に示すAFM像より明らかなように最密充填構造を取っている。この為,AFM探針は探針直下の一個のPSL粒子のみと相互作用しているのではなく,右図にあるように隣接する周囲のPSL粒子とも相互作用をしていると考えられる。そこで,(1)式の拡張を試みた。これより,補正後の相互作用力は下式のように表わせる。
![]()
ここで,Diはi番目のPSL粒子とAFM探針間の距離で, niは距離Diに存在するPSL粒子の数である。表面間距離Diと最小表面間距離D0の比(Di/D0)をciとすると
![]()
で表わされる。
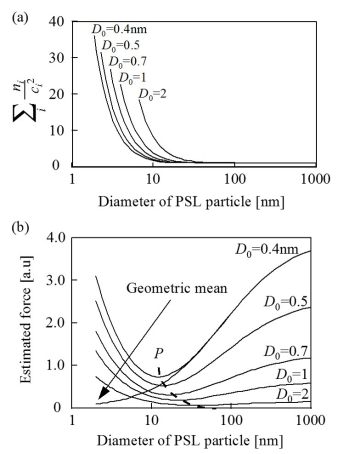
AFM探針とPSL粒子の最小表面間距離D0の最小値は,vdW半径程度と考えられるため,表面間距離D0の最小値は0.4nm程度とした。上式に基づく隣接する各PSL粒子を考慮した相互作用力のPSL粒径依存性を右図 (a), (b)に示す。右図 (a)のように,隣接するPSL粒子の影響の項(![]() )は,PSL粒子の粒径が20nm以下になると,PSL粒子の粒径の減少に伴い増加している。その結果,相互作用力も,PSL粒子の粒径20nm以下で増加している。これは,PSL粒子の粒径が無限小において最密充填している場合の極限,およびPSL粒子の粒径が無限大に増加したときの極限が,共に平面として近似されることを意味している。また右図(b)にあるように,表面間距離D0が長くなるに従って相互作用力は小さくなるが,右図中に示した付着力の極小点PにおけるPSL粒子の粒径が大きくなっている。これは,粒子表面の凹凸に対し表面間距離D0が大きくなった為,相対的に表面凹凸の影響が減少した為と考えられる。ジャンプインはAFM探針とPSL粒子が離れている際に生じることから,表面間距離D0はジャンプアウトに比べ大きいと考えられる。実測値に対するカーブフィットを右図にて行った。これより,ジャンプイン時の近距離引力の値は, D0=4nmにおいてシミュレーションした相互作用力のPSL粒径依存性とほぼ一致した。従って,ジャンプイン時の近距離引力には,隣接しているPSL粒子の相互作用の影響が強く反映されていることが考えられる。
)は,PSL粒子の粒径が20nm以下になると,PSL粒子の粒径の減少に伴い増加している。その結果,相互作用力も,PSL粒子の粒径20nm以下で増加している。これは,PSL粒子の粒径が無限小において最密充填している場合の極限,およびPSL粒子の粒径が無限大に増加したときの極限が,共に平面として近似されることを意味している。また右図(b)にあるように,表面間距離D0が長くなるに従って相互作用力は小さくなるが,右図中に示した付着力の極小点PにおけるPSL粒子の粒径が大きくなっている。これは,粒子表面の凹凸に対し表面間距離D0が大きくなった為,相対的に表面凹凸の影響が減少した為と考えられる。ジャンプインはAFM探針とPSL粒子が離れている際に生じることから,表面間距離D0はジャンプアウトに比べ大きいと考えられる。実測値に対するカーブフィットを右図にて行った。これより,ジャンプイン時の近距離引力の値は, D0=4nmにおいてシミュレーションした相互作用力のPSL粒径依存性とほぼ一致した。従って,ジャンプイン時の近距離引力には,隣接しているPSL粒子の相互作用の影響が強く反映されていることが考えられる。
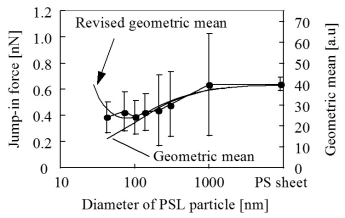
一方,ジャンプアウトが起きる表面間距離D0は,前述のように0.4nm程度と考えられる。上の右図(b) のシミュレーション結果で,D0=0.4nmにおける補正された幾何平均半径のPSL粒径依存性は,PSL粒子の粒径が20nmまで幾何平均半径と同じである。従って,右図のように,粒径20nm以上のPSL粒子とAFM探針間に作用するジャンプアウト時の付着力は,隣接しているPSL粒子の相互作用の影響は小さく,PSL粒子の接触変形の影響が支配的であると考えられる。PSL粒子の変形および隣接しているPSL粒子の影響の他に考慮すべき点として,分子レベルでの凹凸(ミニチップ)の影響,AFM探針先端の球近似の限界などが考えられる。
AFM探針とPSL凝集粒子間に作用する付着力と近距離引力をフォースカーブを用いて測定し,PSL粒子の粒径依存性に与えるPSL粒子の変形の寄与と隣接粒子の影響について解析した。ここで,微粒子系での力の粒径依存性の観点からDMT理論によるvdW力の幾何平均半径の補正を提案した。ジャンプアウト時の付着力は,AFM探針との接触により変形したPSL粒子の半径を1.7倍と補正することで,DMT理論式により理解できた。一方,ジャンプイン時の近距離引力は,隣接している周囲のPSL粒子とAFM探針との相互作用の影響を考慮した補正式により理解できた。実際の半導体表面への微粒子付着現象の解析にも有効な知見を与えている。
信頼性評価
コーティング膜の信頼性を解析する
塗膜は工業製品として重要な地位を占めているが、様々な欠陥や不良が特性劣化の原因となっている。これらの劣化の主要因は、熱、静電気、応力および紫外線などである。製品の信頼性および劣化モデルを構築することは、塗膜に限らず重要である。劣化モデルは活性化エネルギーを基本として考察できる。近年、加速試験の分野も充実しており、製品の寿命予測技術も確立されている。しかし、集積回路素子などの特殊な場合を除いて、食品、機器などの加速試験を全数行うことは稀である。ここでは、劣化モデル、活性化エネルギー、加速試験、寿命予測といった製品の信頼性に関わる内容について述べる。
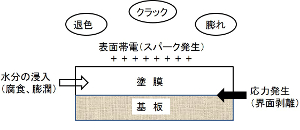
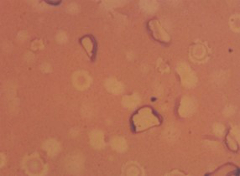
下の左図は塗膜の故障(劣化)モデルの一例を示している。基板上に堆積された塗膜断面において、界面への水分浸透や膜表面の帯電などが起因して欠陥が生じる。また、これらの欠陥から新たに亀裂や腐食等が始まる。塗膜と基板との応力ミスマッチも劣化の原因となる。よって、製品の故障解析においては、塗膜および界面に起因する劣化を区別する必要がある。下の右図は塗膜の劣化写真を示している。塗膜表面の微細クラックや、水分浸透による膨潤が多数確認できる。このように、塗膜の劣化には様々なモードがあり、これらは活性化エネルギーに基づく経時変化として表せる。
物質の劣化の主原因は熱やスパークなどに起因する反応現象である。劣化の進展は、その反応が始まる閾値となる活性化エネルギーに依存する。ここでは、アレニウスの経験的化学反応速度論に基づいて、その概要を述べる。化学反応速度Kは、以下の式で表すことができる。
![]()
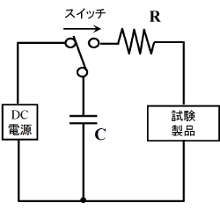
ここで、ΔE:活性化エネルギー (kcal / mol)、B:活性化エネルギー(eV) 、k:ボルツマン定数である。下の左表は一般的な不良が生じる際の活性化エネルギーを示している。活性化エネルギーが低いほど、その不良は生じやすい。各不良が生じるには、活性化エネルギーを超える外部エネルギーの供給が必要である。たとえば、薄膜のピンホールの原因は、スパーク等であり人体との接触により生じる。下の右表は人体および衣類などから生じる帯電量などをまとめている。ワイシャツや作業服などの帯電量は数キロボルトに及んでいる。このような局所的な高電圧により、指が塗膜に触れることで帯電電荷が塗膜へ移り放電が生じる。このような接触放電を試験する方法がある。右図は人体からの帯電電荷の放電試験回路である。人体に相当する静電容量C=200pF、抵抗R=10 kΩとした並列回路により構成している。これらの設備により、人体からのスパークに起因した塗膜の静電耐久性が評価できる。


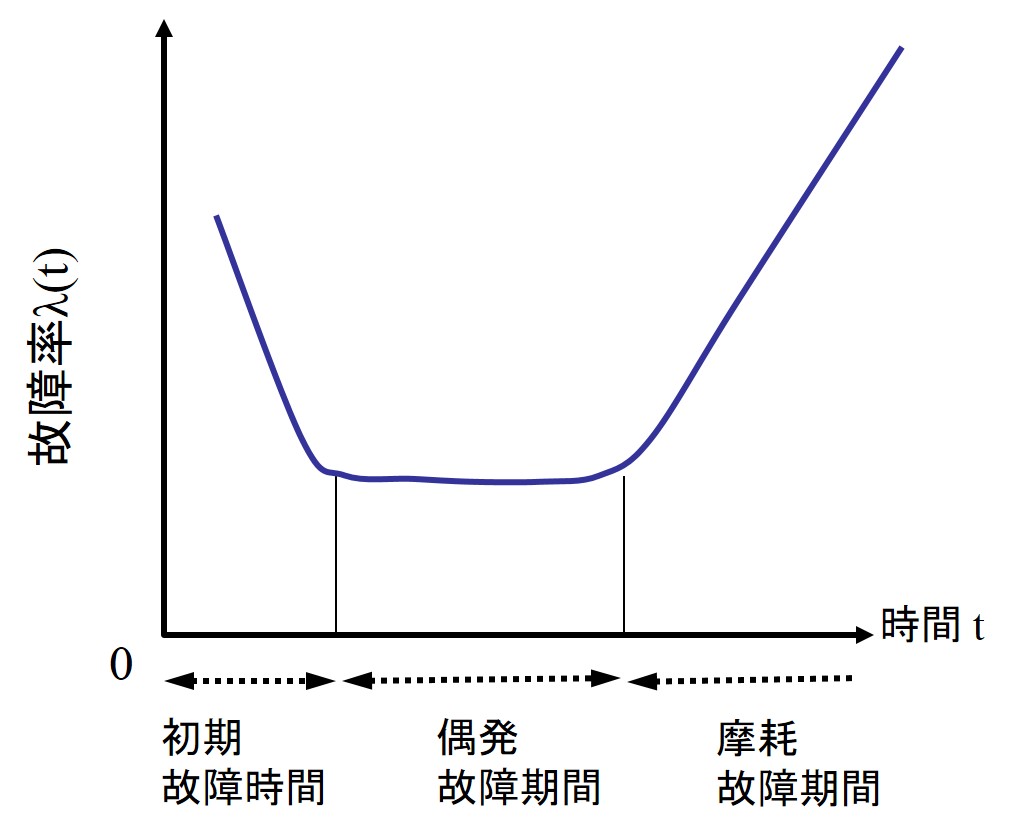
このように、製品の劣化は、活性化エネルギーに基づき生じる。実際の故障の発生率は、その環境下での時間経過に大きく依存する。右図は、製品の使用時期に対する故障発生頻度を表すバスタブ曲線を示している。その曲線の形がバスタブ(風呂釜)に似ているため名づけられた。製品の不良発生は、一般的に、初期不良、偶発不良、摩耗不良の3段階のステージが存在する。製品の初期不良は、使用開始直後に生じる不良であり、作製時に含まれていた不良が原因となっている。これは時間の経過とともに急速に減少する。製品の信頼性を向上するには、まずは初期不良を撲滅する必要がある。実際の生産管理においては、加速試験を実施して初期不良品を除外して出荷する。一方、偶発故障はランダムに生じる不良である。この故障は、製品の性能に起因した故障であり、この範囲内で使用することが望ましい。また、摩耗故障は、寿命に基づく故障として判断され、耐用寿命に近づくことで急激に増加する。製品の信頼性を高くするには、偶発故障率を低く、かつ、摩耗故障率に至るまでの期間が長いことである。
バスタブ曲線に基づいて故障発生頻度は説明できる。ここでは、故障メカニズムに基づく故障密度関数f(t)について述べる。故障分布確率f(t)は、指数分布、正規分布、ワイブル分布が代表的である。
まず、以下の式で表される指数分布について説明する。
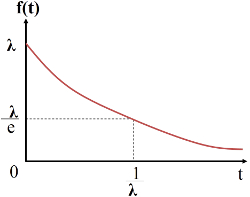
![]()
ここで、λは故障率であり、良品に対する不良品の割合で定義される。多くの場合、故障率λは時間に依存せず一定である。この関数は右図のように表される。すなわち、時間経過とともに故障分布確率f(t)が低下する。また、この分布は、特定の不良要因に依存せずランダムに生じる不良を示す。バスタブ曲線においては初期故障に相当する。
以下の故障分布関数は正規分布となり、一般的な寿命に基づく摩耗故障を表している。
![]()
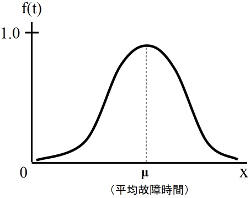
ここで、δは標準偏差であり、μは平均故障時間である。右図ように、ある時期に集中して不良が生じる場合に相当している。
以下の式はワイブル分布であり、一般的な故障解析に多く適用される関数である。製品内に点在する欠陥の中で、最も早く壊れる点によって決定される「ウィークリンクモデル」として理解される。
![]()
ここでmは形のパラメータ、t0は尺度のパラメータ、γはパラメータを表す。実際の故障分布をワイブルチャートにプロットすることでmの値が求められる。そして、m=1の場合は、λは一定となり指数分布となり偶発故障に相当する。また、m>1の時は、λは増加関数となり、正規分布関数に近づき摩耗故障に相当する。そして、m<1ではλは減少関数となり初期故障に相当する。このように、故障状況をワイブル関数で解析することにより、バスタブ曲線の故障モードを診断することができる。
信頼性技術に基づいて、製品の寿命や故障確率を定量的に求めることは産業上で重要である。近年では、食品から電化製品に至るまで、細かく消費期限や保証期間が提示されている。ここでは、どのように製品の寿命を試験し予測可能となるのかを述べる。一般的に加速試験法とは、外部ストレスを加えて製品劣化を加速させることである。そして、評価時間の短縮が可能となり、実用条件下での寿命予測や故障予測を行う。この試験法には、一定ストレスを加えて故障時間分布を観測する定ストレス法と、 一定時間毎にステップ状でストレスを増加させ、故障発生を観測するステップストレス法とがある。下図はこれらの試験法の概略を示している。外部ストレスとしては、一般的に、環境温度および湿度、圧力、荷重などが選択される。
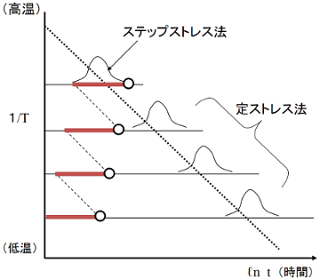
以上の加速試験の結果、以下の考えにより、製品の寿命が求められる。まず、標準使用条件として、温度T0を考え、その時の寿命がL0であるとする。そして、加速状態(ストレス状態)での温度と寿命をT1、L1とする。これらには、以下の関係式がある。
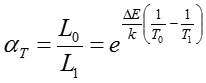
ここで、αT および⊿Eは、加速係数および活性化エネルギーである。よって、定常状態での寿命L0は以下のように表せる。
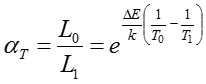
この手法は、塗膜の欠陥発生時間や退色時期の管理、および変形ひび割れなどの様々な耐性変化に適用できる。
ここでは、塗膜の信頼性解析技術について、故障モデル、発生確率、活性化エネルギー、寿命予測といった点に注目し紹介した。昨今、技術の安全性および信頼性の確保は最優先の課題となっている。信頼性といった言葉が一般的となり社会の注目度も高い。近年では、安全および信頼性分野が一つの学問体系として位置付けられており、この観点における技術者養成も重要となっている。
参考文献
- URL: http://kawai.nagaokaut.ac.jp
- 初等信頼性テキスト、日科技連
プリント基板接着層の疲労耐久試験
車載搭載用プリント基板分野において、基板と金属配線を接続する接着層は、振動による疲労破壊が問題となる。疲労破壊では、破壊限界以下の荷重において、繰り返し荷重による亀裂などの疲労が蓄積し、最終的に破壊に至る。近年の電子機器の発達に伴い、はんだ接合部の熱疲労が原因のクラック発生が問題とされてきた。また、近年、車両の電装化に伴って接着剤は車載用電子デバイスの用途が増加している。たとえば、ギヤボックスコントロールユニットやカーナビ等のデバイスなどの多くのセンサーにフレキシブルプリント回路(FPC)が搭載されている。このFPCの性能は接着剤によって性能が左右されるため、接着層の研究はより重要である。車載用デバイスにおいて接着層は1Hz~1kHz程度の振動に晒される環境下にありながら、人の安全のために高い信頼性が求められる。そのため、接着層にかかる様々な周波数の応力振動に対してその疲労特性を検討する必要がある。そこで接着層に様々な振動周波数を与えることで、疲労破壊に対する振動周波数の影響を考察する。また、通常の疲労試験で用いられる正弦波とは異なり、負荷振動を印加することで疲労評価方法の高機能化が期待できる。

まず、引張せん断試験により引張速度依存性を確認し、次いで、周波数の異なる負荷振動を試料に加えてその疲労特性を解析する。試料は右図に示すように銅/フェノール基板の銅表面とポリマーフィルムを接着剤によって接着させたものである。接着剤はシアノアクリレートを主成分とし、これを銅表面に塗布した後にポリマーフィルムをのせて加圧することで接着させた。せん断試験は引張試験機を用いて右図aのように行った。せん断速さを1,10,100mm/minと異なる速さに設定した。疲労試験は右図bのように試料を設置し、固定具下部に振動発生器を用いて負荷振動を掛け、破断するまでのサイクル数を測定した。負荷振動は50, 100, 150Hzの周波数をもつ正弦波を設定し、変位を一定にして行った。
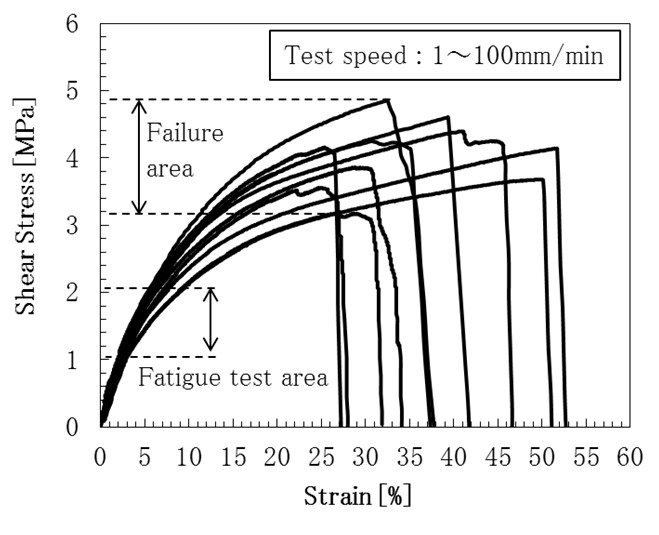
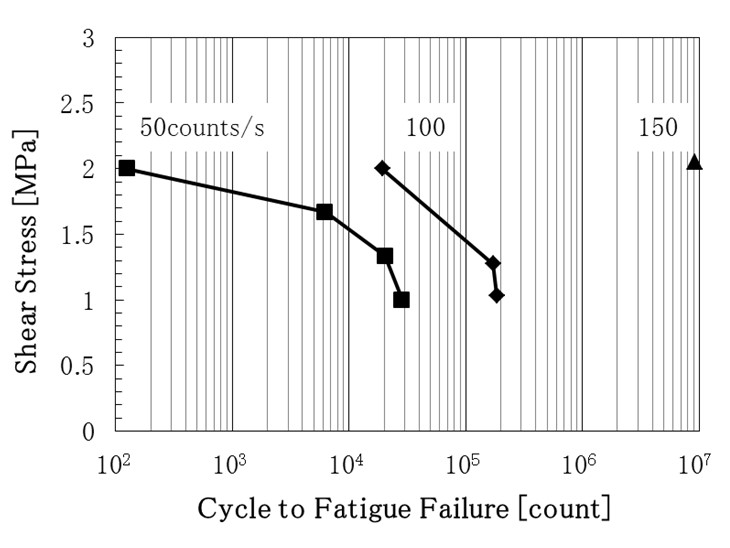
上の左図に引張せん断試験の結果を示す。ひずみが22~51%の変域を持ち、せん断応力が3.1~4.9MPaの変域を持つことが分かる。この結果より、疲労試験では破断されたせん断応力の平均4MPaを基準として、25~50%(1~2MPa)の領域で疲労試験を行った。疲労試験の結果を上の右図に示す。試料に繰り返し生じるせん断応力が小さいほど、疲労破壊までのサイクル数が多いことが分かる。また、振動周波数を高くすることで破断強度が高サイクル側へシフトし、破断までのサイクル数が大きくなっている。疲労の原因として、試料の内部または表面から発生した亀裂が進展することで、比較的低い荷重で破壊されることが考えられる。よって、周波数が大きいほど内部のクラック発生が抑えられたと考えられる。また、接着層は高分子材料特有の粘弾性を示すため、振動周波数を赤くするほどより弾性的な振る舞いを示すと考えられ、これらが接着層の疲労蓄積に影響したと考えられる。以上のように、プリント基板接合の疲労解析において、周波数が増加すると疲労破壊までの繰り返し数が増える傾向が見られた。このことから接着層の粘性挙動が疲労現象に寄与していると考察できる。