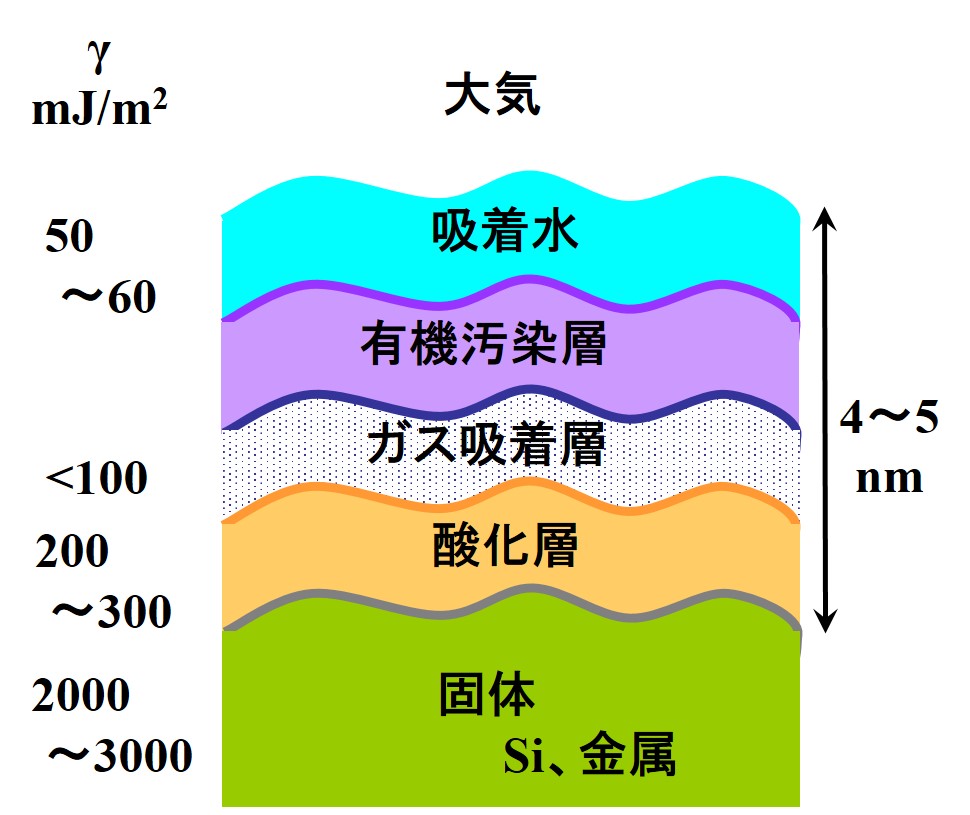
液体および固体の表面には、表面エネルギーγと呼ばれる有限のエネルギーが存在する。表面エネルギーの定義は、物質の表面に存在する単位面積あたりのエネルギーでありJ/m2の単位で表される。この表面エネルギーが、物質の変形や亀裂などの力学的仕事として、あるいは酸化や汚染などの化学的反応として消費される。下図は固体の表面エネルギー変動について説明している。金属などの固体の本質的な表面エネルギーは2000~3000 mJ/m2であるが、酸化層、汚染層、吸着水などの表面層形成により、100 mJ/m2以下に低下する。ここで、表面エネルギーの低下は物質表面の安定化を意味している。すなわち、この表面エネルギーの変動が付着やコーティングといった機能的な仕事をする。表面層の厚さは通常4~5nmである。一方、ある物質の立体形状が決まれば、その表面積Sと表面エネルギーγの積により、物質表面が有するエネルギーの絶対値γ・S(J)が求まる。熱力学的には、定圧・定温の条件下では、このエネルギー(エンタルピー)が最小になるように現象が進行する。すなわち、同一体積の物質であれば、その表面積を最小にするように変形することとなる。液滴が球形になりやすいのは、この理由に基づいている。
一方、表面エネルギーγの単位J/m2は換算するとN/mとなり、下表のように表面張力と呼ばれる力学的作用を表す。表面エネルギー(スカラー量)と表面張力(ベクトル量)とは、数値は同じであるが物理的意味が異なる。すなわち、物質の表面エネルギーが、亀裂や変形などの力学的仕事として消費される場合は「表面張力」として表現するのである。水の表面エネルギー(張力)は72.8mJ/m2であり、エタノールは22.3mJ/m2である。この表面エネルギーの値には、液体分子の分極性が強く反映されている。水分子のように双極子モーメントが高く、分子間相互作用が高い液体の表面エネルギーは高くなる。

ここで、表面エネルギーとサイズ効果について考える。微小サイズの物質に特有な現象として、下式に表される形状サイズ効果がある。すなわち、半径rの微小球を考えた場合、サイズの縮小に伴って、内部エネルギーEC[J]に対する表面のエネルギーES[J]の比率(表面の寄与率A)が高くなることである。
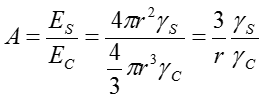
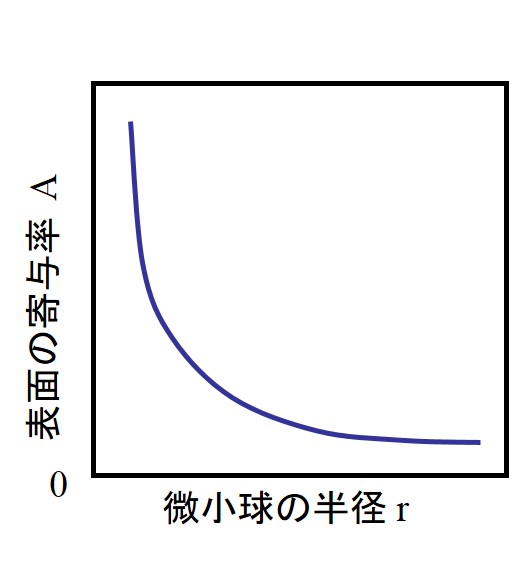
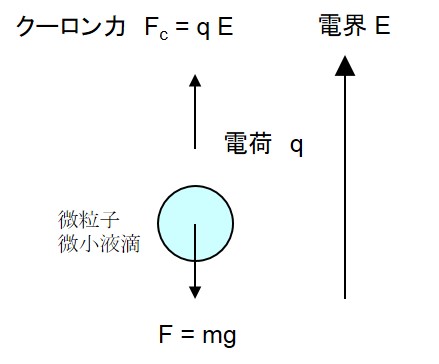
ここで、γCとγSは、それぞれ微小球の凝集エネルギー(J/m3)、および表面エネルギー(J/m2)を表す。γCおよびγSに球の体積および表面積をそれぞれ乗じることにより、エネルギーの絶対値が求められる。よって、下の左図のように、体積が同一のままで、微小球のサイズが縮小した場合、凝集エネルギーに対する表面エネルギーの占める割合が、球の半径rに反比例して増大することが分かる。すなわち、同一体積の微粒子の全てが半径rの微粒子に分割された場合、全体の表面積が飛躍的に大きくなる。よって、微小領域では、体積に基づく現象よりも表面の関与する現象が支配的になる。たとえば、下の右図にあるように、微粒子や微小液滴は、重力よりも表面の帯電や気流の影響を受けて、大気中を落下することなく永続的に浮遊することができる。雲や霧を構成する微小液滴などが浮遊するのは、この原理に基づいている。
近年のナノテクノロジーの発展において、我々はマテリアルの表面特性に注目する必要がある。マクロサイズにおける常識や経験は通用しない場合があり、表面特性を上手に制御していくことが重要となる。
参考文献