表面エネルギーはコーティング、濡れ、付着・剥離などの表面利用技術の基本となる物理量である。これらは、Youngの式などの基本式により、定量的に説明できることを前回述べた。ここでは、接触角計を用いた固体および液体の表面エネルギーの測定方法と利用技術について述べる。表面エネルギーは、分散成分と極性成分の和として表すことができ、これらの成分には表面の化学的性質が反映されている。さらに、コーティング膜や微粒子の溶液中の付着性を議論できる拡張係数Sについて述べる。また、表面処理を行うことで、表面エネルギー成分を変化できる。O2プラズマ処理とシランカップリングなどの様々な実用的な表面処理技術を紹介する。
固体および液体には有限の表面エネルギーが存在しており、それが変形や亀裂などの力学的仕事、酸化や汚染などの化学的反応として消費される。金属などの固体の理想的な表面エネルギーは2000~3000mJ/m2であるが、酸化層、汚染層、吸着水などの表面層形成により、100mJ/m2以下に低下する。ここで、表面エネルギーの低下は表面の安定化を意味している。表面層の厚さは通常4~5nmである。この表面エネルギーが付着やコーティングといった機能的な仕事をする。表面エネルギーは、分散成分γdおよび極性成分γpの和として表される。
γ=γd+γp
分散成分は物質の密度、分子量、硬さなどが反映した物理量であるが、その大小関係は逆である。酸化物や金属の分散成分は低いが、有機材料の場合は高くなる。また、極性成分は、表面の極性基密度や活性度をそのまま反映している。固体および液体の分散成分は「ゼロ」にならないが、極性成分は「ゼロ」になりうる。ここで、各成分を表面同士の分子間相互作用で考える。右図に示すように、分散成分は2個の無極性分子(双極子)間のクーロン引力として表され、London分散エネルギーと呼ばれる。一方、極性成分は、永久双極子間(Keesom)及び、永久双極子-無極性双極子間(Debye)エネルギーとして定義される。これらの成分は、以下の式によって表される。
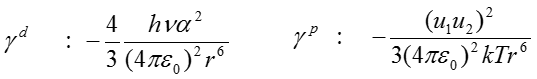
ここで、r は双極子間距離、αは分極率、u は双極子能率、Tは温度である。極性成分は温度Tに反比例することが分かる。たとえば、水の表面エネルギーは室温では72.3mJ/m2であるが、80℃では62.6mJ/m2に低下する。温水での洗浄効果が上がる理由は、この極性成分の低下が理由である。一方、大気などの気体の表面エネルギーは実態がないため「ゼロ」として扱い、成分図上では原点が気体に相当する。
物質の表面エネルギーの分散および極性成分の測定法について述べる。固体(S)と液体(L)との付着エネルギーWaは以下となる事を述べた。
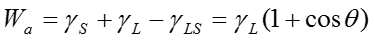 (1)
(1)
ここで、θは固体表面での液体の接触角である。また、付着エネルギーWaは、表面間の相互作用として、各成分間の二乗平均として表せる。
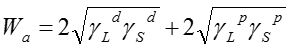
よって以下のYonng-Dupreの式が得られる。
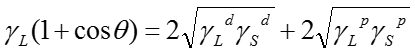 (2)
(2)
ここで、両辺を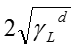 で割る事により下式のように変形できる。
で割る事により下式のように変形できる。
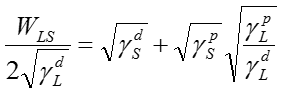 (3)
(3)
まず、(3)式を用いて、未知である固体の表面エネルギー成分を求める。最初に、分散および極性成分が既知である液体を用いて、固体上の接触角を測定する。液体には、極性成分の高い純水と分散成分の高いヨウ化メチレンを用いる。これらの液滴の分散および極性成分を下の左表に示している 。よって、式(3)に基づくと、下の右図のプロットが得られる。
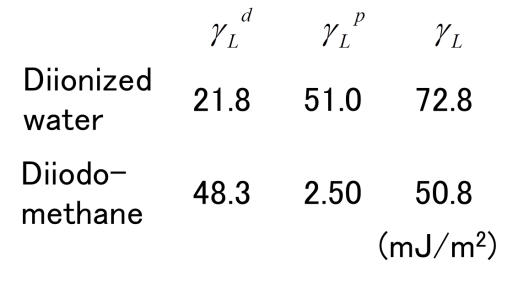
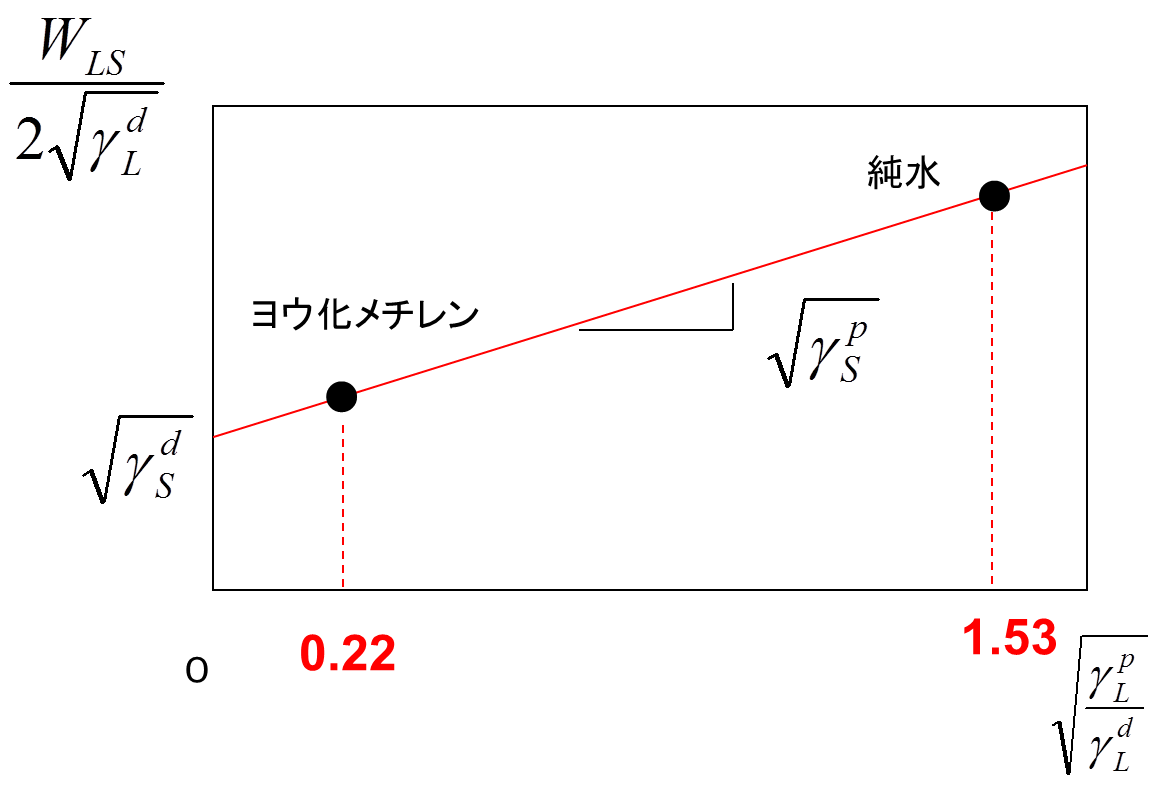
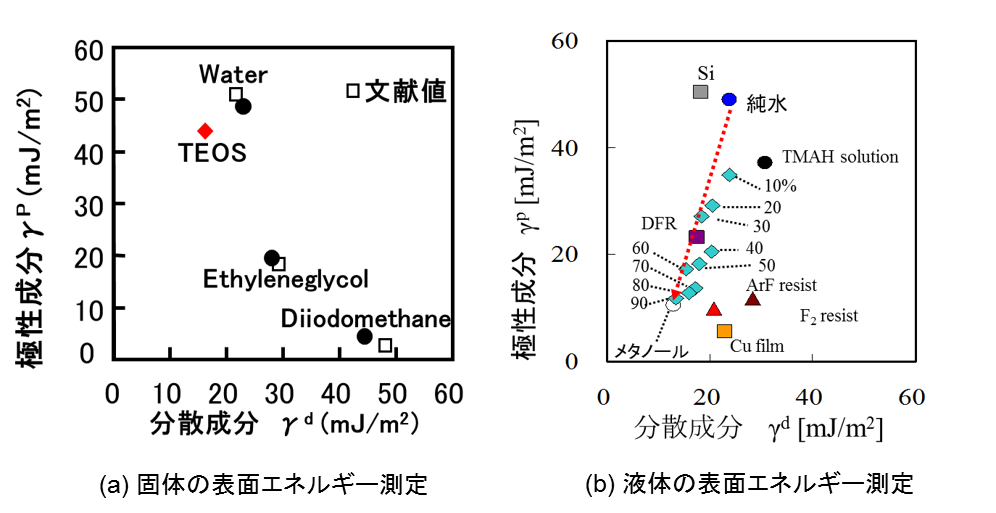
図の切片より固体の表面エネルギーの分散成分γSdが得られ、傾きから極性成分γSpが得られる。また、得られた成分の和として、固体の表面エネルギーγsが求まる。下図(a)は、この手法で求めた表面エネルギーの成分図を示している。横軸に分散、縦軸に極性成分をとり、図中の1点は物質の成分値を表す。ここでは、実際に測定したSiO2膜(TEOS)の成分値を示している。液体として、純水、ヨウ化メチレン、エチレングリコールも示している。SiO2膜と純水の極性成分が高いが、ヨウ化メチレンなどの有機溶剤の分散成分は高いことが分かる。
次に、未知の液体の表面エネルギー成分を求める手法を述べる。ここでは成分が既知の固体としてパラフィンを用いる。パラフィンの表面エネルギーは24.4mJ/m2であり、極性成分が「ゼロ」であるために、分散成分もγSd=24.4mJ/m2となる。よって(2)式の右辺の第2項は「ゼロ」となり、以下の式が得られる。
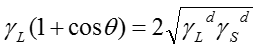 (4)
(4)
パラフィン膜上で液体の接触角θを測定し、表面張力計でγLを測定することにより、(4)式から液体の分散成分γLdが求まる。極性成分γLpは、表面エネルギーγLから分散成分γLdを引いて求まる。このようにして求めた液体の表面エネルギー成分値を上図(b)に示す。ここでは、純水にメタノールを重量wt%で混合した場合の成分値の変化が分かる。Si基板やTMAH水溶液(強アルカリ現像液)、樹脂系高分子、Cuメッキ膜表面の成分値も示している。
ここで(2)式を変形すると、以下のように界面エネルギーγSLが求まる。
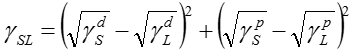
これは、下の左図のように、成分図を平方根でプロットすると、界面エネルギーγSLは2点間の距離として定義できる。また、原点からの距離は、それぞれの表面エネルギーに相当する。この図において、原点を中心とした同じ円周上の物質は同じ表面エネルギーを有することとなる。しかし、その分散および極性成分は異なる。以上のように、接触角法により、物質の表面エネルギーの分散成分と極性成分を求める事ができる。
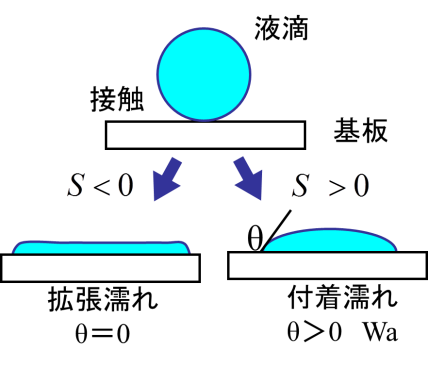
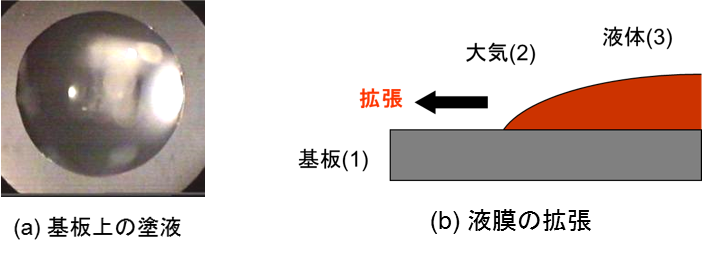
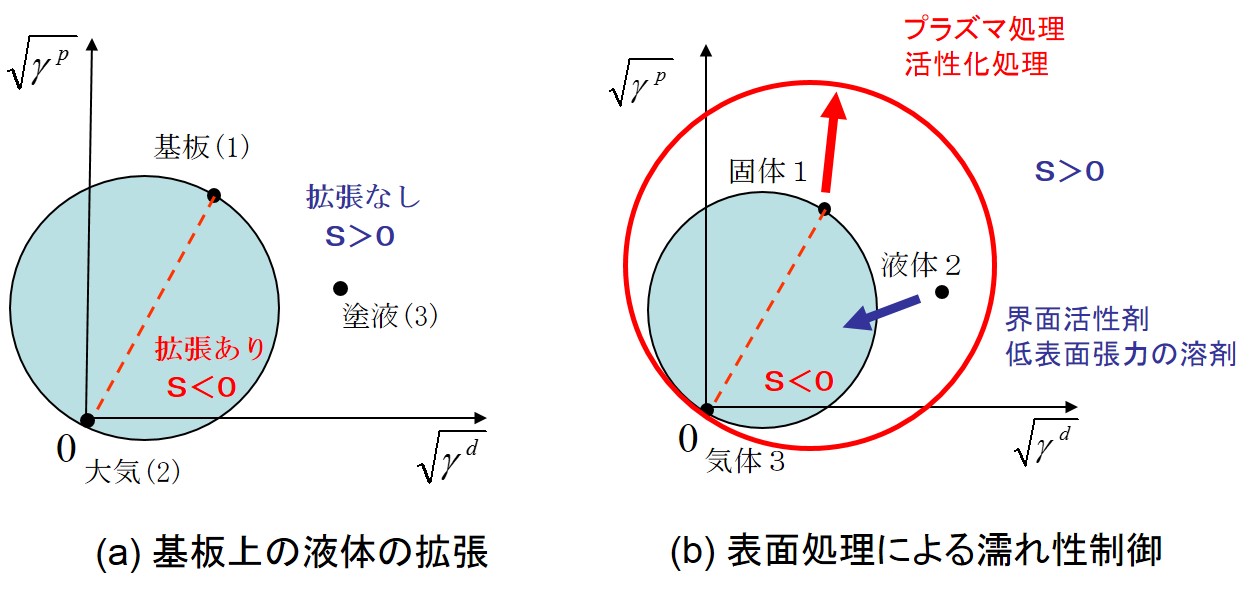
固体上を液体が濡れ拡がる時、大きく2つの濡れモードに分けられる。それは拡張濡れと付着濡れである。上の右図は、これらの濡れ挙動を図示している。拡張濡れの場合、基板に接触した液滴は、基板表面を限りなく拡がり薄い液膜を形成する。この場合、接触角を形成せずθ=0である。一方、基板表面で有限の液滴の接触角( θ>0)を形成する場合を付着濡れと呼ぶ。これらの濡れ現象は、以下の拡張係数S(mJ/m2)で表される。
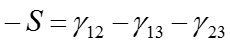 (5)
(5)
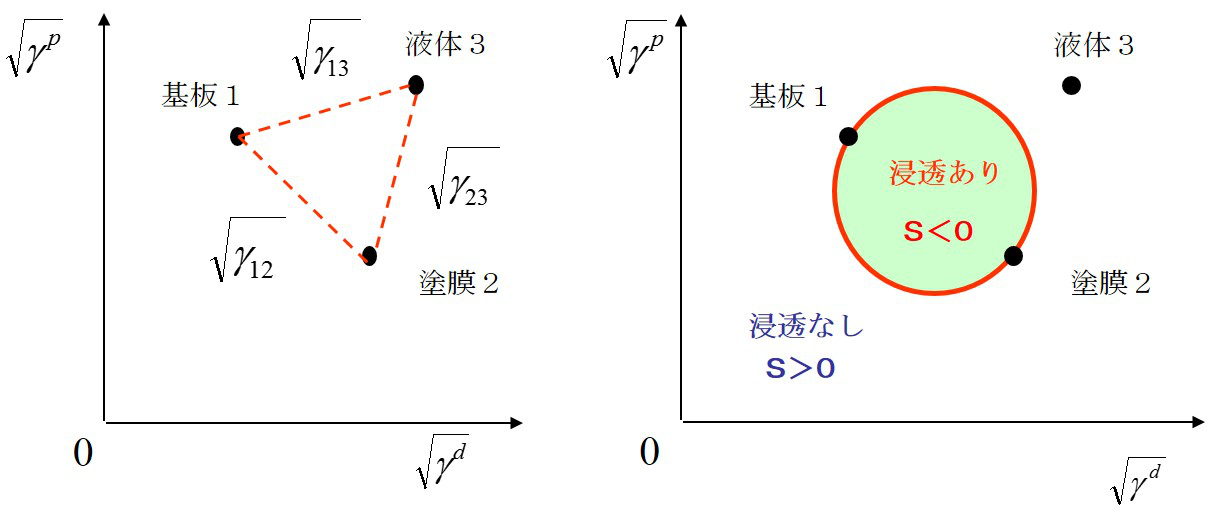
この場合、下図(a)のように、添え字は基板(1)、大気(2)、液体(3)となる。2つの濡れモードは拡張係数Sの符号によって区別され、S<0の場合は拡張濡れとなり、S>0の場合は付着濡れとなる。(付着濡れのエネルギーは、(1)式に従う。)
ここで、(5)式を変形すると以下の(6)式が得られる。
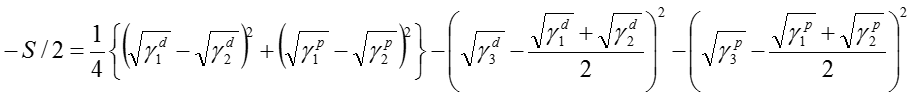 (6)
(6)
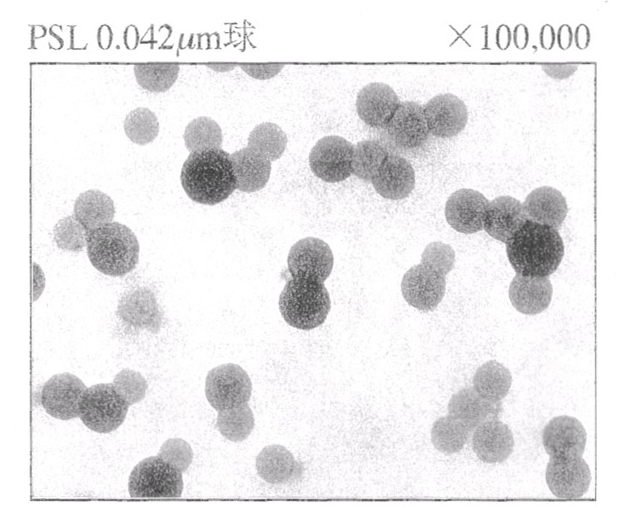
そして、S=0とおくと以下のような円の式となる。
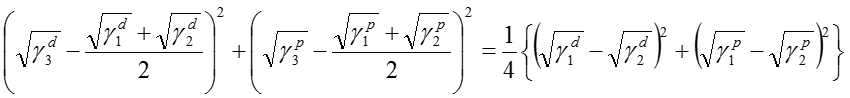
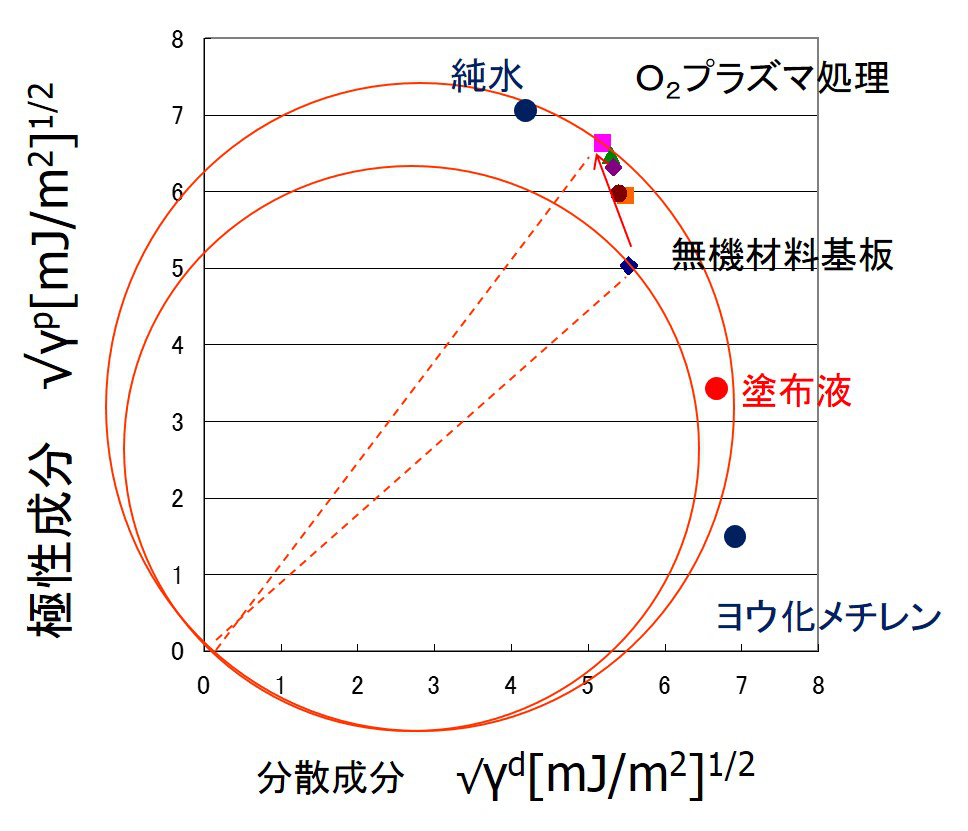
この式は、下図(a) のように平方根の成分図で円として表される。円周上はS=0の成分値を表す。基板上を塗液が拡がる現象は、すでに存在する気体と基板との界面に塗液が侵入するモデルとして扱う。そこで、基板(1)と大気(2)の点を直径とする円を描くと、式(6)で表される円が描ける。液体である塗液(3)の成分値が円内にある場合は、S<0となり拡張濡れとなる。よって、塗液は基板と大気との界面に浸入し自ら拡がる。これは、清浄なガラス基板上をアルコールが拡がる場合や、LB膜が水面を単分子膜で展開する現象として知られている。また、下図(a)のように、塗液の点が円外にある場合は付着濡れモードとなり、塗体は有限の接触角を有した液滴を形成する。ほとんどのコーティングは付着濡れモードである。実際の塗液の成分値を右図に示す。有機溶剤を多く含む塗液は分散成分が高くなり、そのままでは円内に入らないため、金属やガラス表面などの無機基板上では拡張しない。塗液の成分値を円内に入れるには、下図(b)のように界面活性剤などを添加して極性成分を下げる場合と、プラズマ処理などにより基板の極性成分を高めることが効果的である。右図の例では、O2プラズマ処理を行うことで、無機材料基板の極性成分が増加したため、塗布液の成分値が円内に入っている。このように、表面エネルギー成分図を用いることで、塗液のコーティング性の制御方法が説明できる。
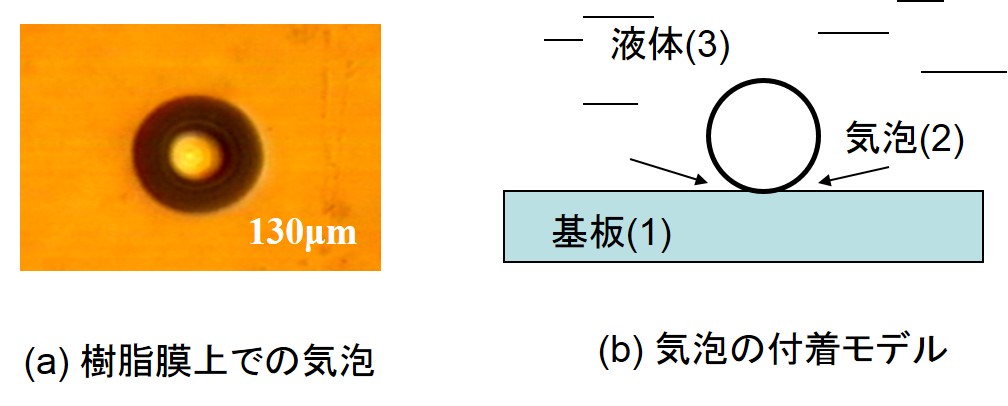
基板上の塗液の広がりは、下の左図のように、液中での気泡の除去性にも適用できる。有限の体積の大気が気泡であるため、(6)式がそのまま適用できる。すなわち、液体の成分値が円内に入れば、気泡は基板から遊離する。また、円外であれば気泡は除去されない。以上は熱力学的な取り扱いであるが、超音波振動などの外部エネルギーを印加すると気泡は除去される。微小気泡の付着性コントロールは、メッキプロセス、洗浄、撹拌、発泡、ウェットエッチングなどの様々な産業的分野において重要である。
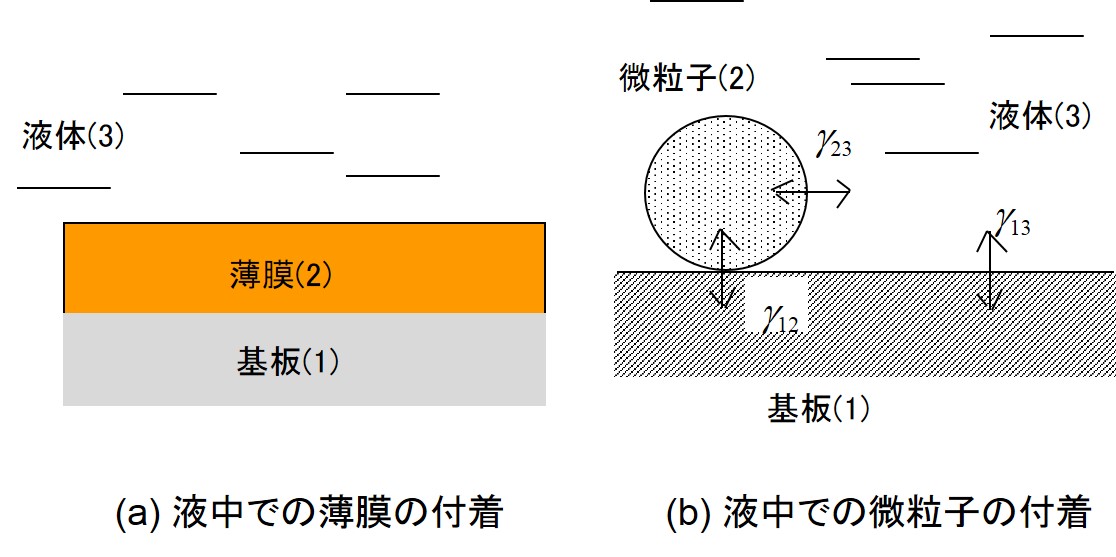
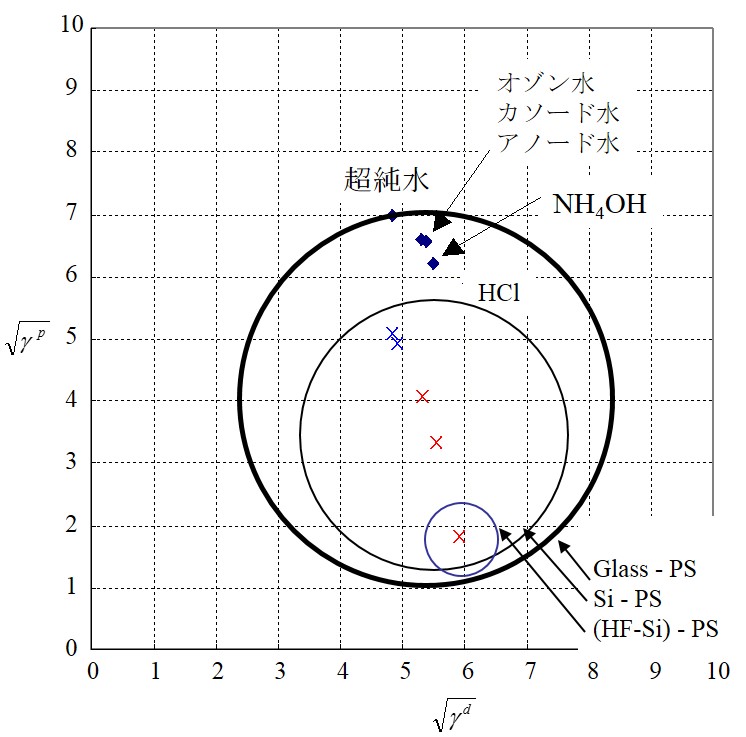
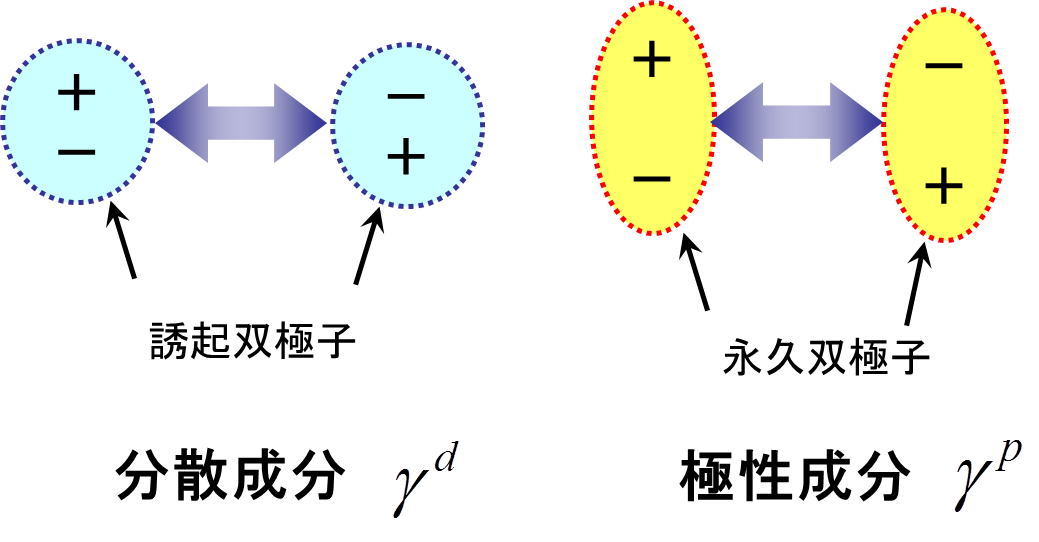
拡張係数の理論は、液中でのコーティング膜や微粒子の付着性に応用できる。液中あるいは高湿度下での塗膜の剥離は、上の右図(a)のように、基板(1)と塗膜(2)間の界面に液体(3)が浸入することを意味する。上の右図(b)のように、基板上に付着した微粒子についても同様に取り扱える。解析手順は、下の左図のように、基板と塗膜を直径とした円を描き、そこに液体の成分値が円内に入るか否かで判断する。ここでは、下の右図のようなPSL(ポリスチレンラテックス)粒子の除去性を検討する。PLS粒子は形状や大きさが揃っており、標準粒子として用いられる。右図にあるように、ガラス基板上に付着したPSL粒子は純水などの液体によって除去できる。しかし、Si基板やHF処理をしたSi基板では、円内に液体の成分値は入らないため、粒子の除去が困難になる。