
固体表面に液滴が触れると、右図のように接触角が形成される。液滴の接触角は、表面エネルギー、や濡れ仕事といった表面の熱力学的なエネルギー収支を反映している。ただ、この接触角は、固体表面の物理量の簡単な測定手法としても有効である。具体的には、固体の表面積や面積割合が、精度高く計測できる。これには、Wenzelの式とCassieの式といった関係式を用いる。これらの式は、Youngの式と並んで固体表面の濡れ性の基本式である。
液体の濡れ性は、固体表面の粗さに敏感である。粗面の濡れ性は、以下のWenzelの式で表せる。
cos θw = r cos θ
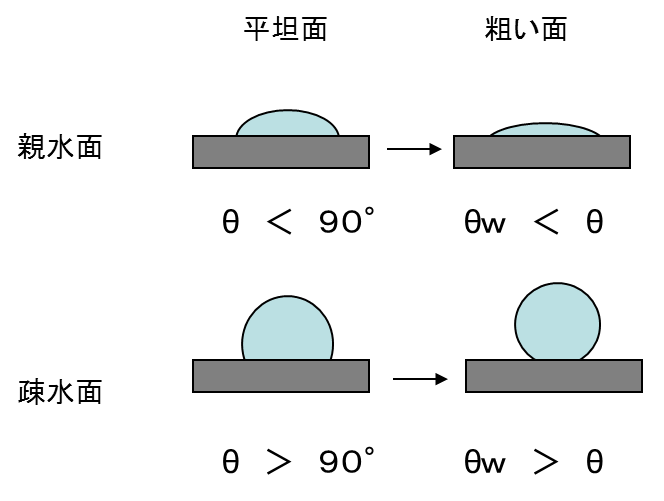
ここで、θwは粗い面上での接触角を表し、θは同じ材質で平坦面での接触角を表す。rは平面に対する粗面の面積比(r≧1)を表す。表面が粗いほど、面積比rは増大する。この面積比に対して、右図のように、濡れ特性を図示できる。Wenzelの式は、θ<90度ではθw<θとなり、θ>90度では、θw>θとなることを示している。すなわち、表面粗さが増加するにつれて、親水性表面では接触角が小さくなり、疎水性表面では接触角がさらに増大する。接着剤や半田付けのように、表面が粗いと濡れやすい現象は、この関係式に基づく。よって、これらのデータベースを構築すれば、下式のように固体の表面積測定が可能となる。
r = cos θw / cos θ
接触角測定の液滴直径は数ミリメータ程度であり、平均的な面積増加率としてrが求まる。一般に、固体の表面積の計測は、レーザー方式や触針式の粗さ計などが用いられる。しかし、このWenzelの式を用いることで、精度高く表面積を測定できる。
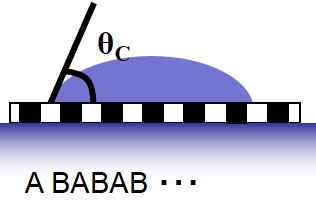
一方、右図のように、異なる材質Aと材質Bで構成された複合表面を考える。Aの材質が占める面積割合をσとする。このとき、複合表面での接触角θcは、以下のCassieの式で表される。
cos θ c = σ cos θA + (1 -σ) cos θB
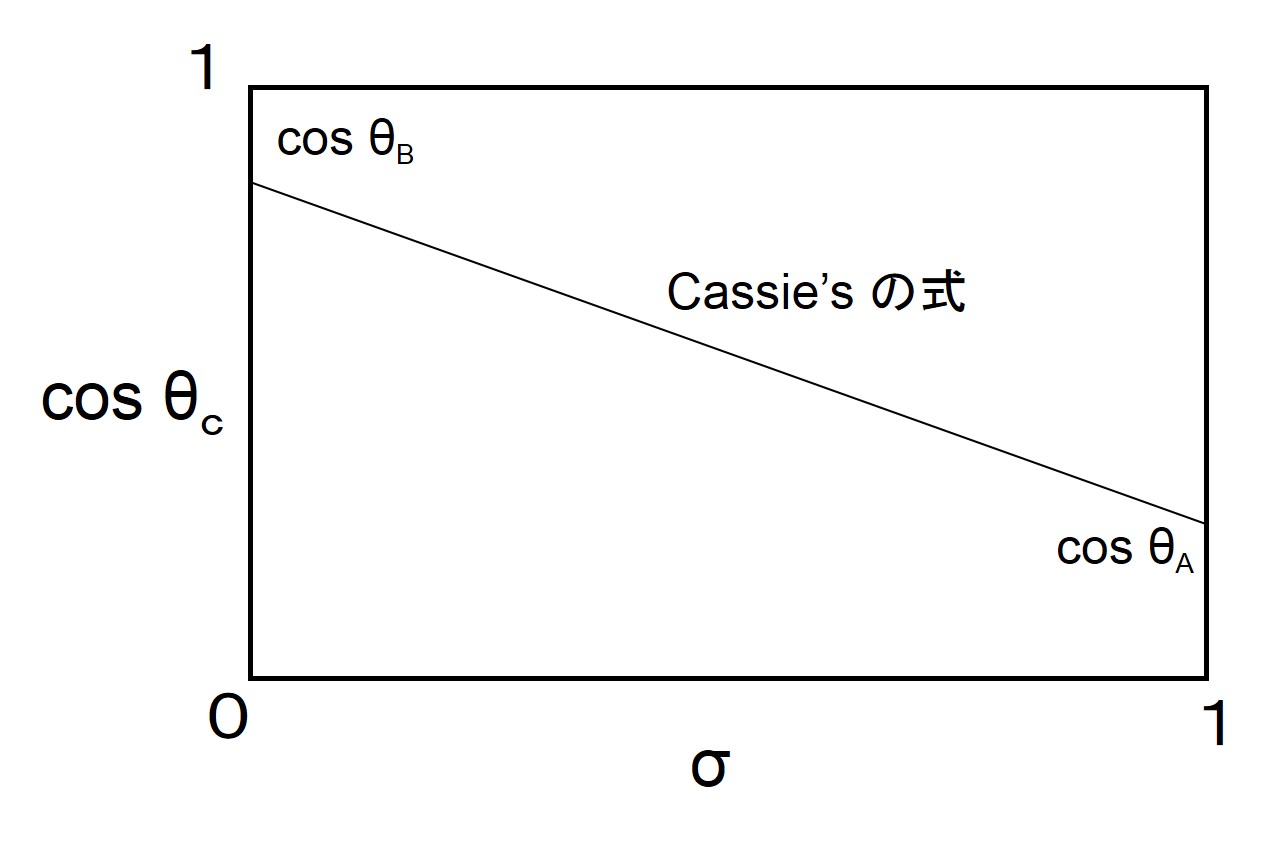
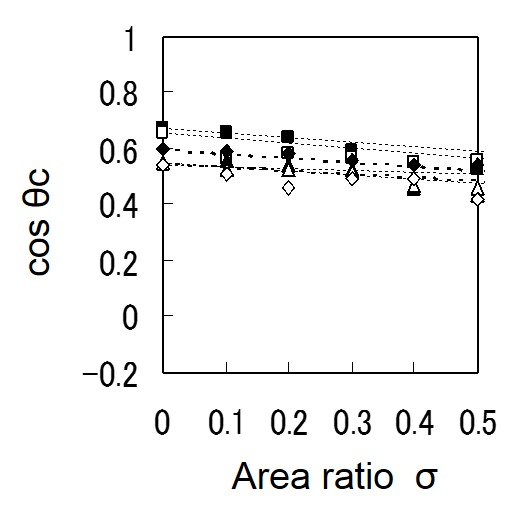
ここで、θAおよびθBは、A基板およびB基板だけでの液滴の接触角である。上の左図および右図は、面積割合σの変化に対する接触角変化を示している。Cassieの接触角θcは、材料の面積割合σに直線的に変化する。よって、下式のように、素材の面積割合σを求めることができる。
σ =(cos θc - cos θB)/(cos θA - cos θB)
通常、材料の面内分析はEPMAやXPSなどの高価な設備を用いる場合が多いが、Cassieの式によれば面積割合を簡単に求めることができる。
以上のように、接触角測定により、固体表面の物理情報を精度良く簡単に求めることができる。
参考文献