濡れを考える場合、液滴の接触角はよく用いられる手法である。この接触角θとはどのような意味を持っているのだろうか?あるいは、どのように使うべきなのか?ここでは、基本原理に立ち返り、本質的な接触角の特性を考える。さて、濡れは面と面との接触における基本概念であり、コーティングや材料合成分野でも重要となる。濡れの概念は液体だけでなく、固体や膜表面においても共通の概念である。材料科学では、濡れと乾燥は、大きいエネルギー変化を伴う現象として理解できる。濡れは熱力学的な平衡状態に基づき基礎理論が構築されている。ここでは、平面での液滴の濡れ挙動を示す基本式として、Youngの式とDupreの式について述べる。
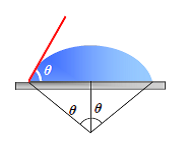
固体基板上での液滴の濡れ性を表す指標に、接触角θがある。接触角法は、測定が簡単であり、汎用性の高い測定法の一つである。液滴の接触角は、接触角計(ゴニオメーター)で測定できる。最近は高精度のマイクロスコープが登場しているため、これを用いた投影測定で十分である。接触角計の誤差は1度以下であり、測定者の差が出にくい長所がある。液滴の接触角は、右図にあるように、液滴を球の一部として仮定した場合、立体球の中心角の半分に相当する。熱力学な定義では、この液滴球の中心角としての定義が本質であり、下図(a)にあるような実験的に得られる接触角は、幾何学的に等価な角度にすぎない。固体平面での濡れ性を表す関係式に、以下のYoungの式がある。
γSV = γLS + γLV cosθ ; cosθ=(γSV - γLS)/ γLV (1)
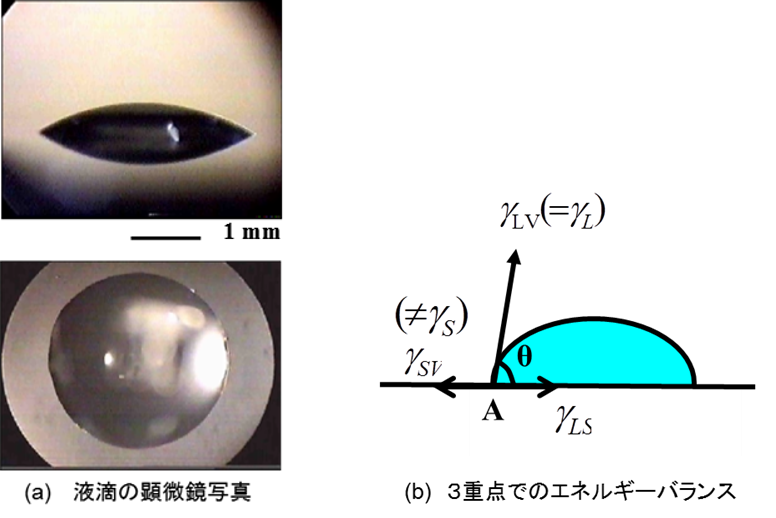
上図(b)にあるように、Youngの式は、固相(S)、液相(L)、気相(V)の3重点において、液滴と固体の表面エネルギーγLV、γSVと液滴と固体間の界面エネルギーγLSで表される。これらは物質の表面有する単位表面積あたりのエネルギー(J/m2)として表される。このときのVはvapor(蒸気)を表しており、接触角測定は液滴の飽和蒸気圧下で行うことを意味している。これは、接触角の経時変化において大きく影響することになる。Youngの式を、3重点における力学的な釣り合いの式として説明する著述が見られるが、これは正しくない。Youngの式は、液滴球の中心角を基本とした表面積および界面積の導出と、各エネルギーのバランスに基づいて導出される。ここで、親水性(θ=0度、cosθ=1)と疎水性(θ=90度、cosθ=0)表面を考える。θ=0度とは、γSV=γLV、(ただしγLS=0)となり、これは親水性を示している。この式から、親水性表面を得るには、基板と液滴の表面エネルギーを近づけるとともに、界面エネルギーを最小にすることが必要である。いわゆる同じ材質同士であれば良く濡れることを表している。逆に、θ=90度とは、(γSV-γLS)<<γLVとなることであり、これは疎水性の濡れ性を示している。疎水性表面を得るには、液体の表面エネルギーを固体よりもできるだけ大きくし、界面エネルギーも増大することが必要となる。Youngの式から、表面エネルギーが同じ値の表面間の組合せであっても、接触角はゼロにならないことが分かる。これは界面エネルギーがゼロではないからである。界面エネルギーをゼロにするには、各物質の表面エネルギーが等しいだけでは不十分である。このためには、表面エネルギーの成分(分散、極性)を等しくすることが必要となる。これら成分の取り扱いについては後述する。以上のように、Youngの式を用いることで、身近な濡れ性を説明することができる。
界面での液滴の濡れ性を議論する上で重要な関係式として、以下のDupreの式がある。
Wa =γSV+γLV-γSL
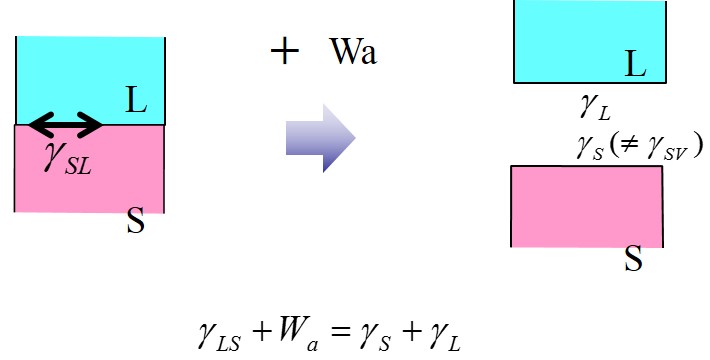
この式は、右図に表されるように、界面が2つの表面へ分離する場合のエネルギー収支に基づいている。ここで、Waは界面を分離するために必要なエネルギー(J/m2)であり、剥離エネルギーと呼ばれる。エネルギーの損失がなければ、Waは付着エネルギーに相当する。また、液滴と固体表面の場合は、濡れエネルギーとして扱われる。以上のYoungの式とDupreの式を組み合わせることで、以下のYoung-Dupreの式が得られる。
Wa =γLV (1 + cos θ) (2)
この式を用いることで、実験的に濡れエネルギーを求めることができる。
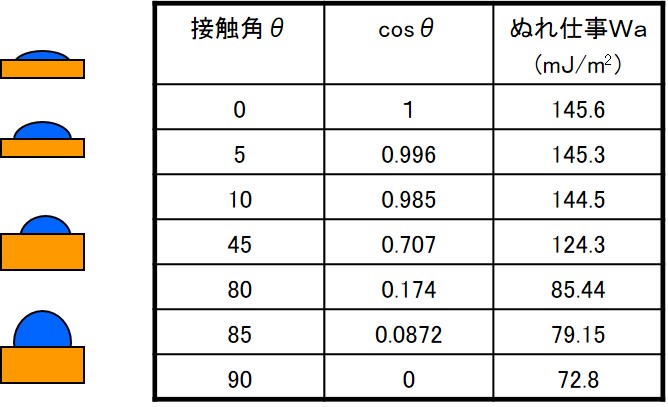
液滴の濡れ性を議論する場合、接触角θの値をそのまま用いるケースが見られる。しかし、接触角だけでは物理的な議論が困難である。少なくとも、(1)式および(2)式を用いて、濡れエネルギーWaとして、現象を解析することが望ましい。下表にあるように、接触角θが0~10度の範囲で変化しても、濡れエネルギーは0.8%程度しか変化していない。よって、接触角が2倍変化しても、表面特性が倍増して変化することにはならない。すなわち、接触角が低い親水表面の場合では、大きい現象変化は見られないことを示している。逆に、接触角が80~90度の範囲となる疎水表面では、濡れエネルギーは17%変化しており、大きい現象変化とみなされる。同じ接触角の変化量であっても、エネルギーの変化としては大きい隔たりがある。以上のように、液滴の濡れ性および付着性を議論する上で、これらの式は基本となる。
固体上での液滴の接触角について、代表的な理論式に基づいて説明した。また、接触角の取り扱いにおける実験的なノウハウについても言及した。コーティング剤などの塗布において、このように濡れエネルギーとして定量化することで正確に理解できる。
参考文献