塗膜は工業製品として重要な地位を占めているが、様々な欠陥や不良が特性劣化の原因となっている。これらの劣化の主要因は、熱、静電気、応力および紫外線などである。製品の信頼性および劣化モデルを構築することは、塗膜に限らず重要である。劣化モデルは活性化エネルギーを基本として考察できる。近年、加速試験の分野も充実しており、製品の寿命予測技術も確立されている。しかし、集積回路素子などの特殊な場合を除いて、食品、機器などの加速試験を全数行うことは稀である。ここでは、劣化モデル、活性化エネルギー、加速試験、寿命予測といった製品の信頼性に関わる内容について述べる。
下の左図は塗膜の故障(劣化)モデルの一例を示している。基板上に堆積された塗膜断面において、界面への水分浸透や膜表面の帯電などが起因して欠陥が生じる。また、これらの欠陥から新たに亀裂や腐食等が始まる。塗膜と基板との応力ミスマッチも劣化の原因となる。よって、製品の故障解析においては、塗膜および界面に起因する劣化を区別する必要がある。下の右図は塗膜の劣化写真を示している。塗膜表面の微細クラックや、水分浸透による膨潤が多数確認できる。このように、塗膜の劣化には様々なモードがあり、これらは活性化エネルギーに基づく経時変化として表せる。

物質の劣化の主原因は熱やスパークなどに起因する反応現象である。劣化の進展は、その反応が始まる閾値となる活性化エネルギーに依存する。ここでは、アレニウスの経験的化学反応速度論に基づいて、その概要を述べる。化学反応速度Kは、以下の式で表すことができる。
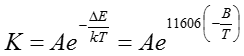
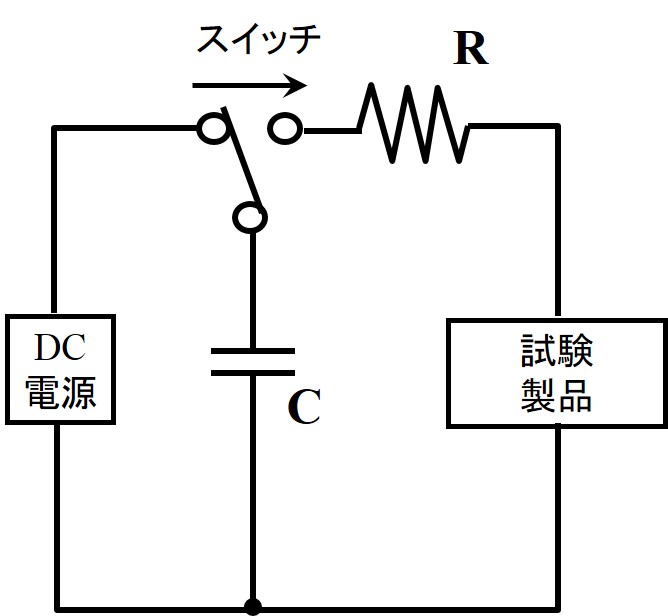
ここで、ΔE:活性化エネルギー (kcal / mol)、B:活性化エネルギー(eV) 、k:ボルツマン定数である。下の左表は一般的な不良が生じる際の活性化エネルギーを示している。活性化エネルギーが低いほど、その不良は生じやすい。各不良が生じるには、活性化エネルギーを超える外部エネルギーの供給が必要である。たとえば、薄膜のピンホールの原因は、スパーク等であり人体との接触により生じる。下の右表は人体および衣類などから生じる帯電量などをまとめている。ワイシャツや作業服などの帯電量は数キロボルトに及んでいる。このような局所的な高電圧により、指が塗膜に触れることで帯電電荷が塗膜へ移り放電が生じる。このような接触放電を試験する方法がある。右図は人体からの帯電電荷の放電試験回路である。人体に相当する静電容量C=200pF、抵抗R=10 kΩとした並列回路により構成している。これらの設備により、人体からのスパークに起因した塗膜の静電耐久性が評価できる。


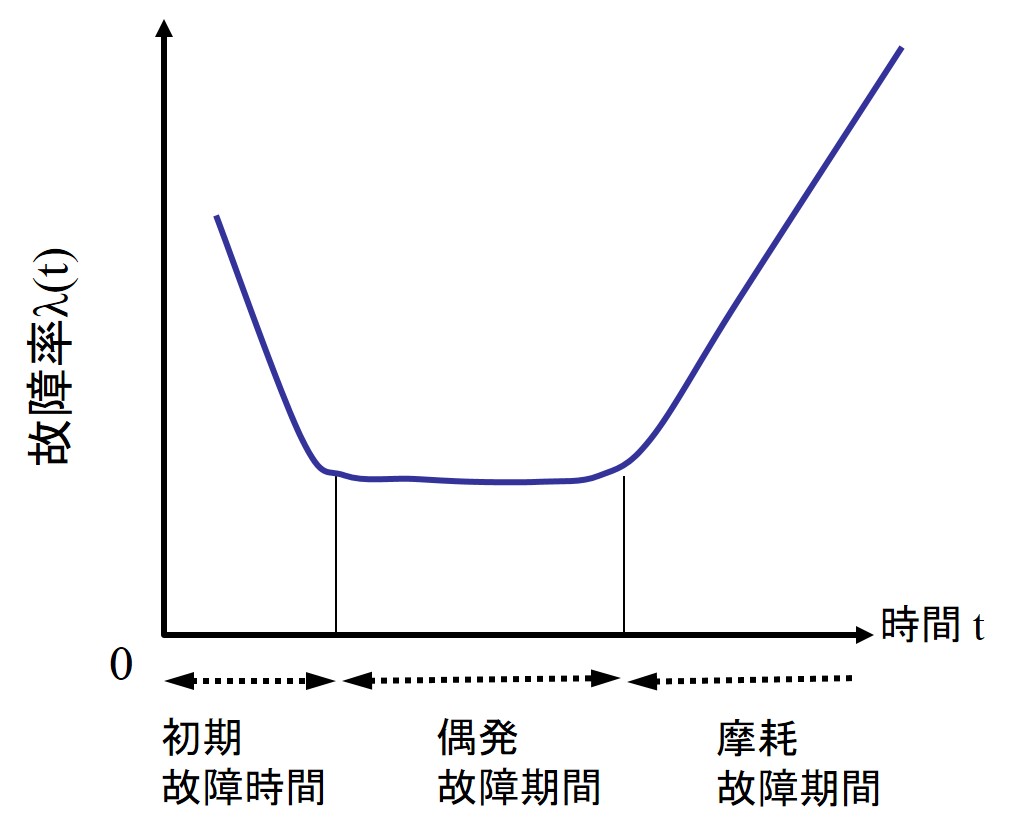
このように、製品の劣化は、活性化エネルギーに基づき生じる。実際の故障の発生率は、その環境下での時間経過に大きく依存する。下図は、製品の使用時期に対する故障発生頻度を表すバスタブ曲線を示している。その曲線の形がバスタブ(風呂釜)に似ているため名づけられた。製品の不良発生は、一般的に、初期不良、偶発不良、摩耗不良の3段階のステージが存在する。製品の初期不良は、使用開始直後に生じる不良であり、作製時に含まれていた不良が原因となっている。これは時間の経過とともに急速に減少する。製品の信頼性を向上するには、まずは初期不良を撲滅する必要がある。実際の生産管理においては、加速試験を実施して初期不良品を除外して出荷する。一方、偶発故障はランダムに生じる不良である。この故障は、製品の性能に起因した故障であり、この範囲内で使用することが望ましい。また、寿命故障は、寿命に基づく故障として判断され、耐用寿命に近づくことで急激に増加する。製品の信頼性を高くするには、偶発故障率を低く、かつ、摩耗故障率に至るまでの期間が長いことである。
バスタブ曲線に基づいて故障発生頻度は説明できる。ここでは、故障メカニズムに基づく故障密度関数f(t)について述べる。故障分布確率f(t)は、指数分布、正規分布、ワイブル分布が代表的である。
まず、以下の式で表される指数分布について説明する。
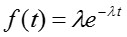
ここで、λは故障率であり、良品に対する不良品の割合で定義される。多くの場合、故障率λは時間に依存せず一定である。この関数は下図のように表される。すなわち、時間経過とともに故障分布確率f(t)が低下する。また、この分布は、特定の不良要因に依存せずランダムに生じる不良を示す。バスタブ曲線においては初期故障に相当する。
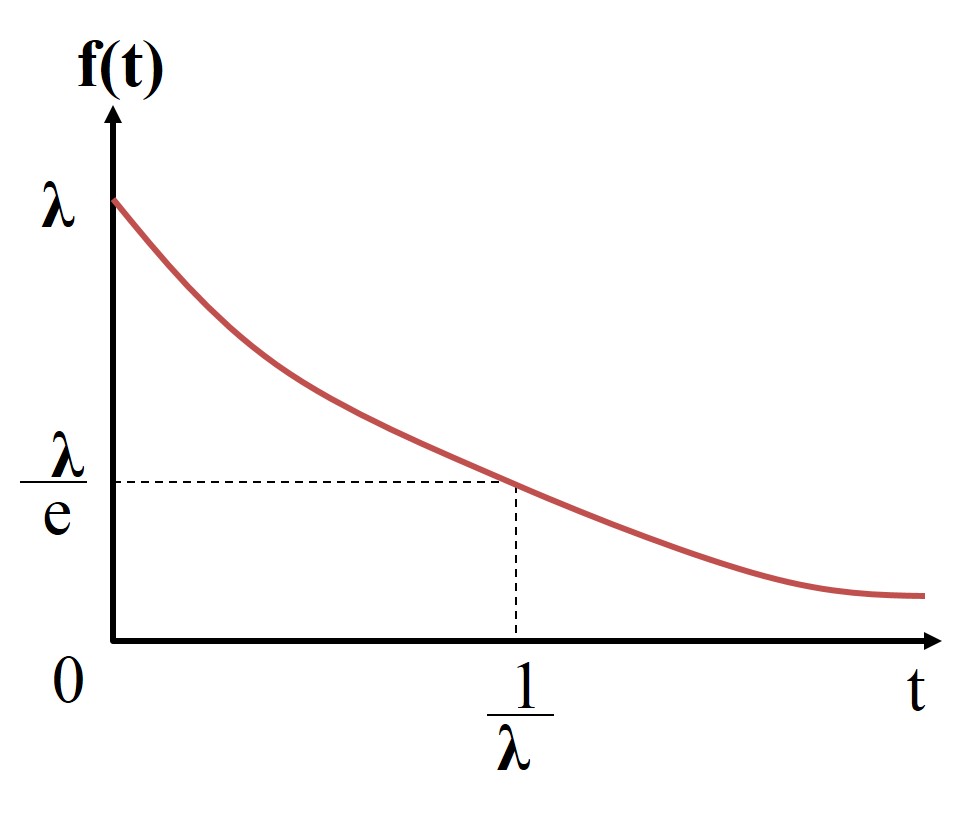
以下の故障分布関数は正規分布となり、一般的な寿命に基づく摩耗故障を表している。
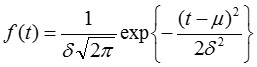
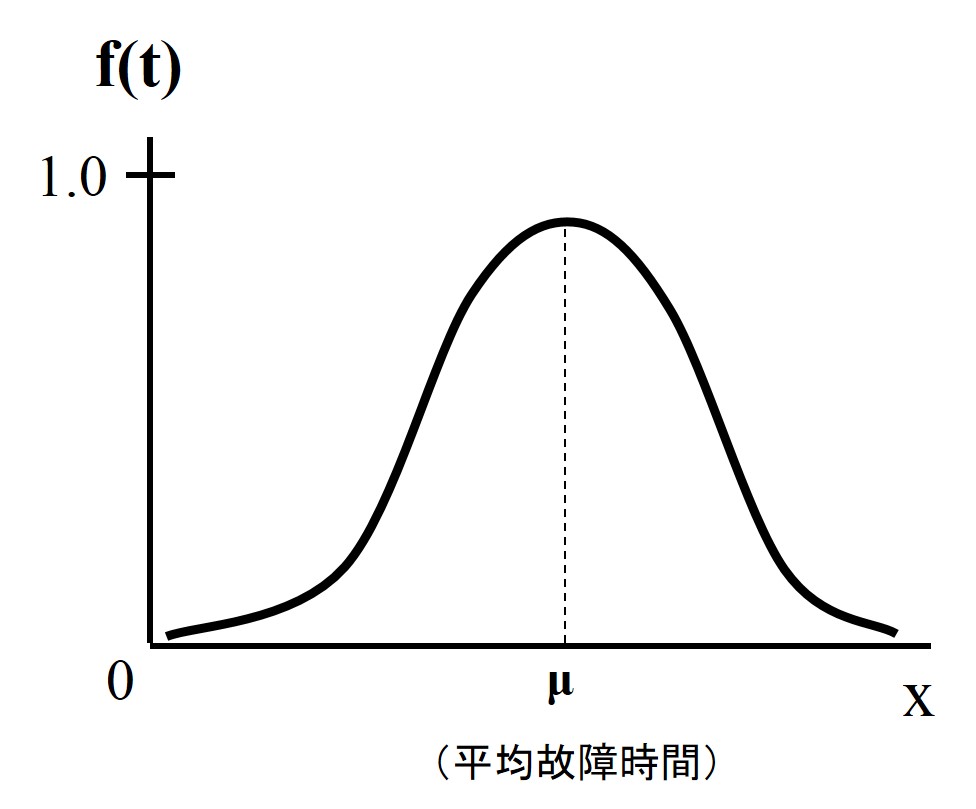
ここで、δは標準偏差であり、μは平均故障時間である。下図ように、ある時期に集中して不良が生じる場合に相当している。
以下の式はワイブル分布であり、一般的な故障解析に多く適用される関数である。製品内に点在する欠陥の中で、最も早く壊れる点によって決定される「ウィークリンクモデル」として理解される。
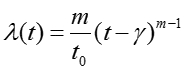
ここでmは形のパラメータ、t0は尺度のパラメータ、γは位置のパラメータを表す。実際の故障分布をワイブルチャートにプロットすることでmの値が求められる。そして、m=1の場合は、λは一定となり指数分布となり偶発故障に相当する。また、m>1の時は、λは増加関数となり、正規分布関数に近づき摩耗故障に相当する。そして、m<1ではλは減少関数となり初期故障に相当する。このように、故障状況をワイブル関数で解析することにより、バスタブ曲線の故障モードを診断することができる。
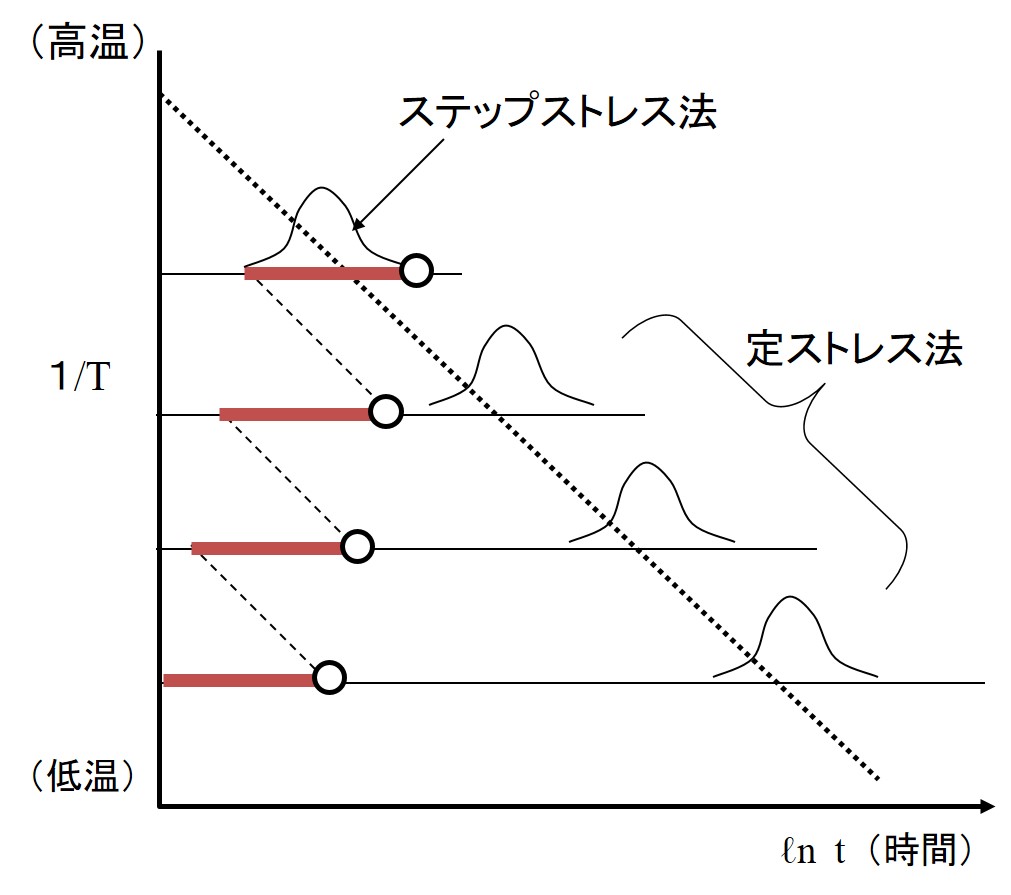
信頼性技術に基づいて、製品の寿命や故障確率を定量的に求めることは産業上で重要である。近年では、食品から電化製品に至るまで、細かく消費期限や保証期間が提示されている。ここでは、どのように製品の寿命を試験し予測可能となるのかを述べる。一般的に加速試験法とは、外部ストレスを加えて製品劣化を加速させることである。そして、評価時間の短縮が可能となり、実用条件下での寿命予測や故障予測を行う。この試験法には、一定ストレスを加えて故障時間分布を観測する定ストレス法と、 一定時間毎にステップ状でストレスを増加させ、故障発生を観測するステップストレス法とがある。下図はこれらの試験法の概略を示している。外部ストレスとしては、一般的に、環境温度および湿度、圧力、荷重などが選択される。
以上の加速試験の結果、以下の考えにより、製品の寿命が求められる。まず、標準使用条件として、温度T0を考え、その時の寿命がL0であるとする。そして、加速状態(ストレス状態)での温度と寿命をT1、L1とする。これらには、以下の関係式がある。
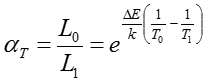
ここで、αT および⊿Eは、加速係数および活性化エネルギーである。よって、定常状態での寿命L0は以下のように表せる。
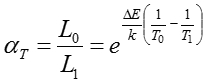
この手法は、塗膜の欠陥発生時間や退色時期の管理、および変形ひび割れなどの様々な耐性変化に適用できる。
ここでは、塗膜の信頼性解析技術について、故障モデル、発生確率、活性化エネルギー、寿命予測といった点に注目し紹介した。昨今、技術の安全性および信頼性の確保は最優先の課題となっている。信頼性といった言葉が一般的となり社会の注目度も高い。近年では、安全および信頼性分野が一つの学問体系として位置付けられており、この観点における技術者養成も重要となっている。
参考文献