微細粒子の付着機構は,原子間力顕微鏡(AFM)の相互作用測定により解析できる。ポリスチレンラテックス(PSL)凝集粒子とAFM探針間に作用する相互作用力の粒径依存性を,乾燥大気中でのフォースカーブ測定により解析できる。粒径42nm~1μmの範囲で,相互作用力の粒径依存性は一般的なDMT理論より導かれる幾何平均の粒径依存性と異なる。相互作用に基づく粒子の変形と隣接しているPSL粒子の寄与の導入により,AFM探針とPSL凝集粒子間の相互作用の測定結果を説明できる。
微粒子の付着要因の一つであるvan der Waals(vdW)力は表面間に作用する相互作用力であり,表面物理,コロイド化学,生化学などの分野を中心に活発に研究が行われてきた。vdW力の理論的な研究には,Hamaker,Derjaguin,Lifshitzのものがある。その後,実験的研究が表面力測定装置(Surface Force Apparatus)などによって行われてきた。近年,原子間力顕微鏡(Atomic Force Microscope, AFM)を用いたvdW力に関する研究は,理論的,あるいは実験的に盛んに行われている。Larsonらのように,直径十μm程度の球状粒子をカンチレバーに取り付け,溶液中での粒子の付着挙動をDLVO (Derjaguin-Landau-Verwey-Overbeek) 理論を用いて解析した報告も多々なされている。また,ジャンプアウト時の付着力と試料の表面自由エネルギーの極性成分との間に,正の相関があることも知られている。
微粒子の付着および凝集挙動は,JKR (Johnson-Kendal-Roberts) 理論やDMT (Derjaguin-Muller-Toporov) 理論に基づき,表面自由エネルギーや弾性率などの物性値を用いて解析できる。しかしながら,膜厚数百nmの薄膜材料の弾性率は,形状効果によってバルクに対して変化すると考えられる。そのため,粒径数百nmの微粒子同士の付着挙動は,粒径数μmの微粒子やバルクの付着挙動と異なることが考えられる。また,Marquardtらは,直径10nm~10μmの金属微粒子の誘電関数がバルクに対して異なることを報告している。一方,微粒子間の相互作用力に関する研究も,近年活発になってきている。例えば,微粒子を主原料とするトナーインクや顔料などの技術分野においては,凝集性や付着挙動が重要になる。またULSI (Ultra-Large-Scale-Integration)プロセスにおいては,設計寸法は10nm以下に迫ってきている。ショート,断線等の歩留まり低下の原因となる付着微粒子のサイズの目安は,デザインルールの1/3程度と考えられる。この為,洗浄プロセスや微細加工プロセスなどにおいては,数nm以下の粒径の微粒子の付着力低減技術の確立が重要になると考えられる。以下,AFM探針先端を球近似し,フォースカーブを用いて,AFM探針と粒径42nm~1μmのポリスチレンラッテックス粒子(Polystyrene latex; PSL)の間に作用するジャンプアウト時の付着力とジャンプイン時の近距離引力の粒径依存性を解析した結果について考察する。DMT理論を基本に,PSL粒子の変形の効果及び隣接しているPSL粒子の相互作用の影響の点を考慮して粒子間の相互作用の理論式を補正し,粒子付着性を検証する。
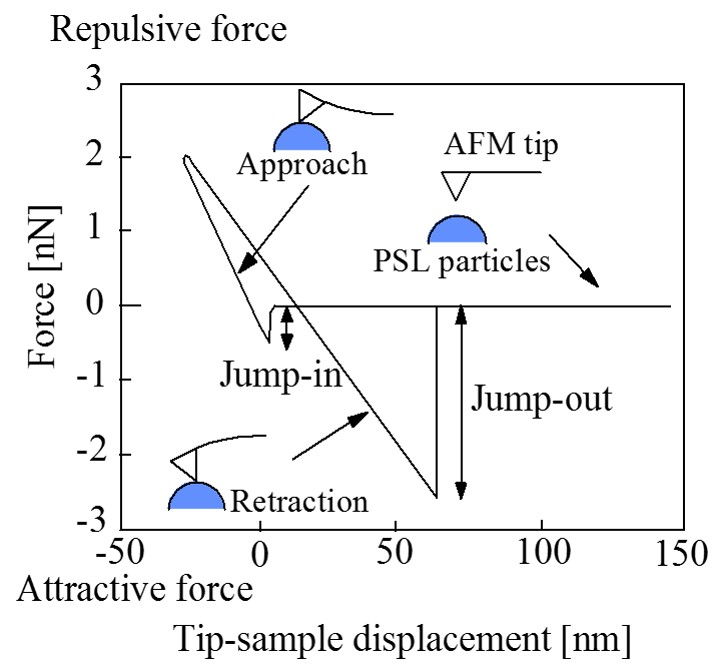
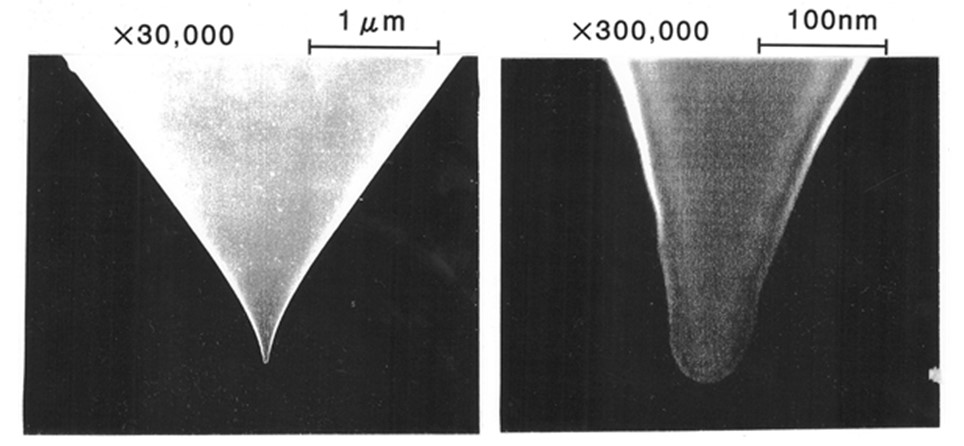
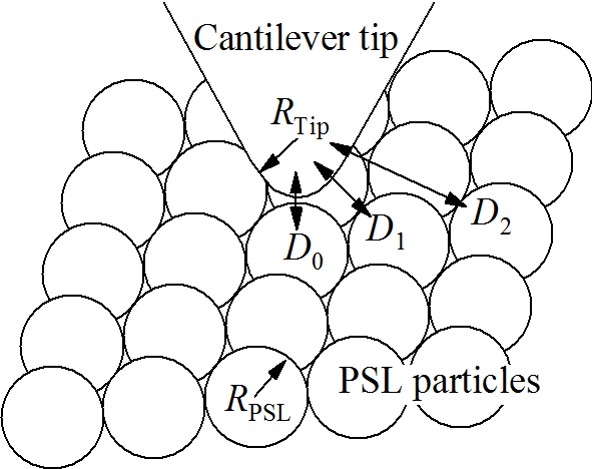
実験として,PSL粒子(日本合成ゴム,STADEXシリーズ)は,平均粒径42, 73, 100, 136, 206, 298, 1001nmのものを用いた。粒径の標準偏差は,それぞれ12.8, 4.79, 2.58, 2.83, 1.81, 1.53, 2.36%である。HF洗浄処理により自然酸化膜を除去したSi(100)waferに,これらPSL粒子の分散された電解液を滴下し,自然乾燥させたものをサンプルとした。バルクのサンプルとして,ポリスチレンシート(PS sheet : 三菱樹脂,ヒシプレート) を用いた。付着力と近距離引力は,AFM(セイコー電子工業(株)製,SPA-300)を用いて,上の左図に示すフォースカーブで求めた。付着力と近距離引力には,それぞれ上の左図中に示すジャンプアウトした時とジャンプインした時の力を用いた。カンチレバーにはサンプルの帯電の影響を除去するためAuコートされたSi3N4(オリンパス光学,OMCL-TR400PB-1,バネ定数0.1N/m)を用いた。上の右図に示すAFM探針のSEM観測の結果,先端曲率半径は40nmであった。吸着水によるラプラス力の影響を除去する為,測定は乾燥雰囲気中(4%RH,20℃)で行った。フォースカーブは,AFM表面像観察の後,AFM探針を任意のPSL粒子の頂点直上セットし測定を行った。付着力と近距離引力は,面内の各PSL粒子に対しランダムに20回行い,平均値及びその標準偏差で評価した。PSL粒子の弾性変形を,二次元有限要素法で解析した。ここでAFM探針とPSL粒子のヤング率はそれぞれ150GPa,2.7GPaとし,ポアソン比はそれぞれ0.24,0.34とした。
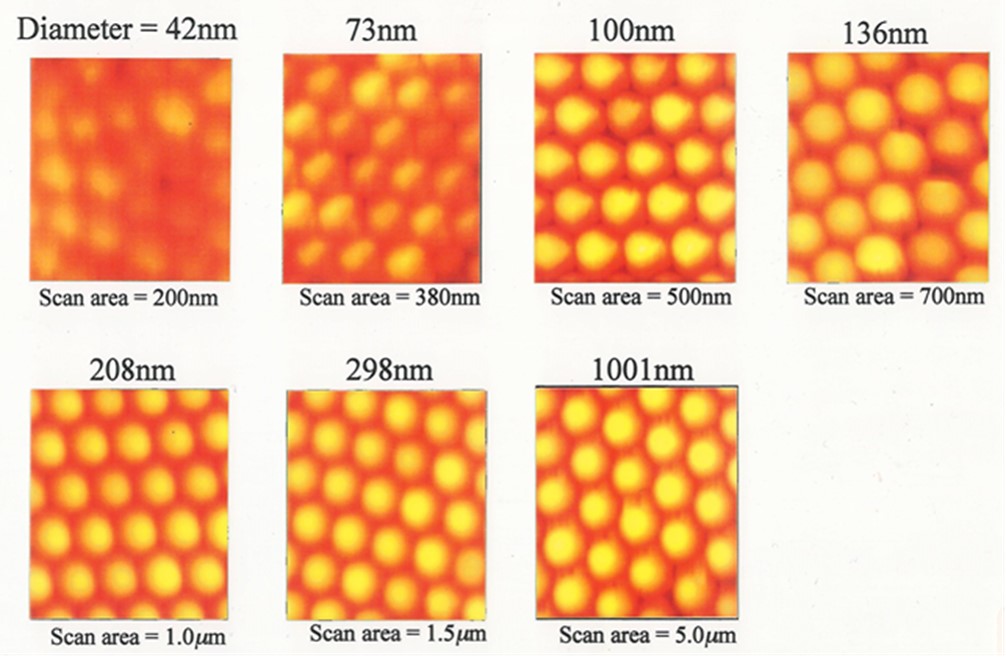
上図は各粒径におけるPSL凝集体のAFM像を示している。各PSL粒子は基板上で最密充填構造をとって凝集している。これらの粒子1個の中心位置において,AFM探針に働くジャンプアウト時の付着力とジャンプイン時の近距離引力を下図(a),(b) に示す。付着力と近距離引力は,粒径の減少に伴い減少することがわかる。
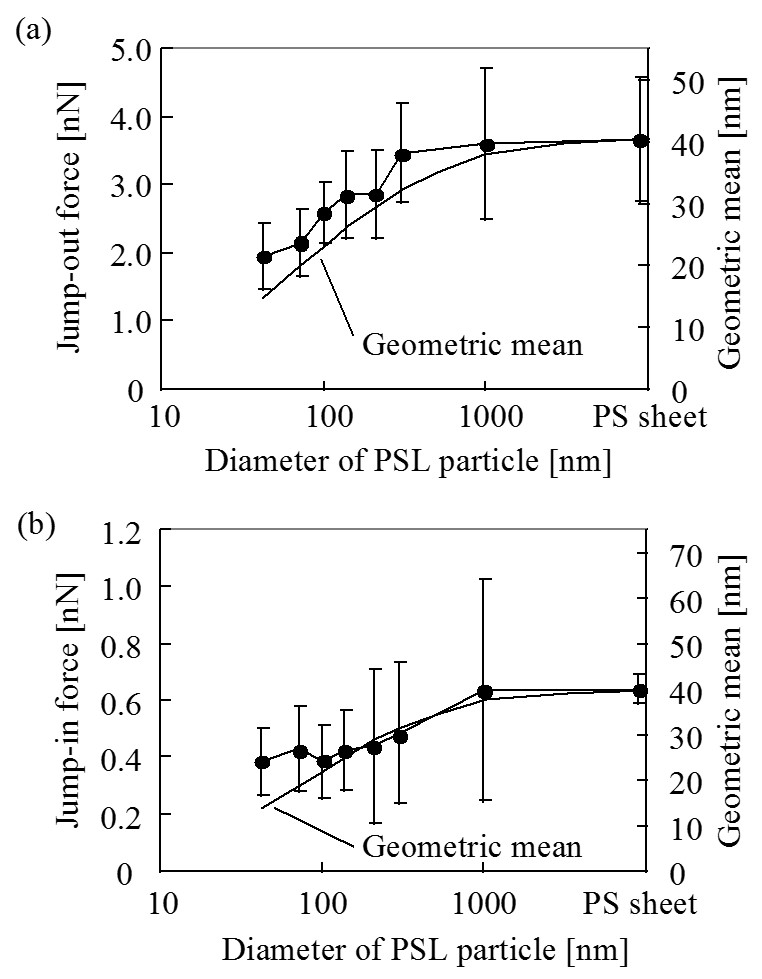
球状粒子間の相互作用力の粒径依存性は,DMT理論により幾何平均半径に比例することが知られている。
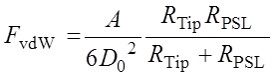 (1)
(1)
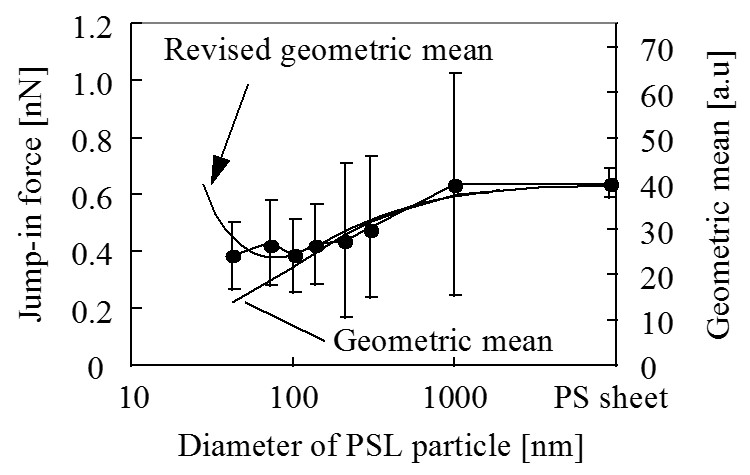
ここで,AはHamaker定数,D0はAFM探針とPSL粒子の最表面間距離,RTip,RPSLはAFM探針の曲率半径とPSL粒子の半径である。PSL粒子の半径,及びAFM探針の先端曲率半径は既知である。測定では同一のAFM探針を用い,サンプルには同一のポリスチレンを用いていることから,Hamaker定数Aを一定と仮定すると,測定系の相互作用力と近距離引力は幾何平均半径を用いて解析することができる。そこで,上式で表わされるvdW力との比較を行う為,上図 (a),(b)に幾何平均半径のPSL粒径依存性を示した。ジャンプアウト時の付着力は,どのPSL粒径についても,上式(RTipとRPSLから計算される幾何平均半径)と比べて大きくなっている。一方,ジャンプイン時の近距離引力は,粒径100nm以上のPSL粒子に対して上式と一致しているが,粒径100nm以下のPSL粒子に対してはジャンプイン時の近距離引力が大きくなっている。
上図(a)において,幾何平均半径の実験値と計算値が合わない原因は,AFM探針との接触によるPSL粒子の変形の寄与によるものと考えられる。そこで,PSL粒子の変形の付着力への効果に関して,以下の考察を行った。
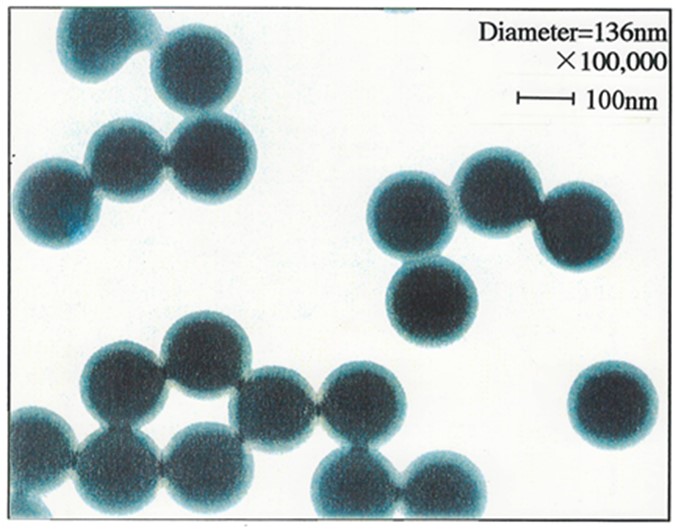
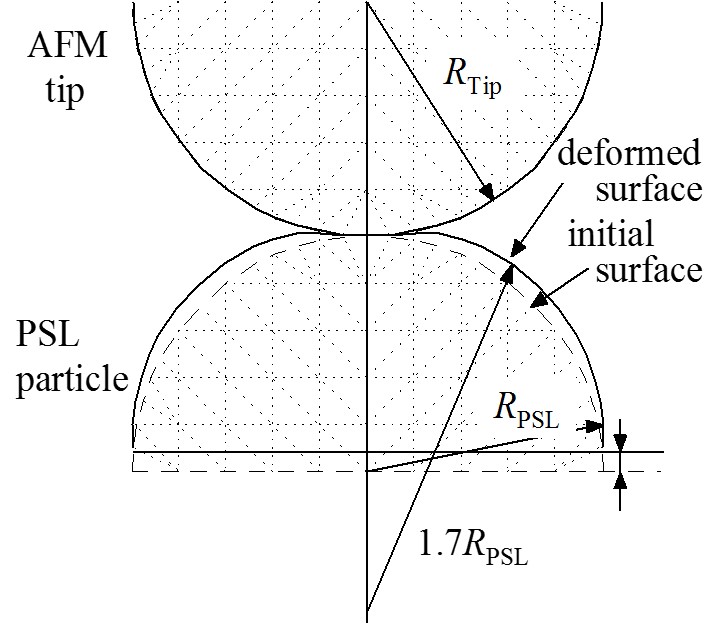
上の左図は,溶液中のPSL粒子のTEM像を示している。上の左図より明らかなように,PSL粒子間の接触面は大きく歪んでいる。これは,vdW引力に起因する付着力の作用で互いに吸着し,接触部でPSL粒子の表面が弾性変形を起こしたためと考えられる。そこでAFM探針との接触変形により変化したPSL粒子の曲率半径を補正する目的で,有限要素法解析によりシミュレーションを行った。シミュレーションした結果を上の右図に示す。ここで,PSL粒子の押し込まれる距離をTEM像と同程度と仮定し,シミュレーションではPSL粒子の半径の10%とした。これより,PSL粒子の歪みによる表面形状の変形が定量化できる。特に接触部付近において,PSL粒子表面の曲率半径は,変形前の半径の約1.7倍に達している。また,PSL粒子の曲率半径はAFM探針との接触点から離れるにつれて減少している。ここで接触変形によるPSL粒子の曲率半径をR*PSLとし,(1)式のPSL粒子の半径RPSLをR*PSLと置き換える。これより,補正後の相互作用力は下式のようになる。
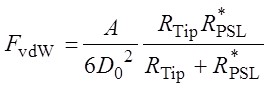
図4 (a) のジャンプアウト時の付着力のPSL粒径依存性にフィッティングした結果,R*PSL≒1.7 RPSLが得られた。 R*PSLを用いて求めた幾何平均のPSL粒径依存性を下の左図に示す。これより,ジャンプアウト時の付着力は,AFM探針との接触により変形したPSL粒子の曲率半径の増加に依存していると考えられる。

ジャンプイン時の近距離引力には,AFM探針の接触によるPSL粒子の変形は影響しないと考えられる。しかし,図4 (b)にあるように, 粒径100nm以上のPSL粒子では,実測値は(1)式に従っているが,それより小さいPSL粒子との近距離引力は,(1)式より大きくなっている。そこで,隣接する周囲のPSL粒子の影響を考察する。
(1)式は,一対の球状粒子間に作用する相互作用力に関する記述である。実験で用いたPSL粒子は,図3に示すAFM像より明らかなように最密充填構造を取っている。この為,AFM探針は探針直下の一個のPSL粒子のみと相互作用しているのではなく,上の右図にあるように隣接する周囲のPSL粒子とも相互作用をしていると考えられる。そこで,(1)式の拡張を試みた。これより,補正後の相互作用力は下式のように表わせる。
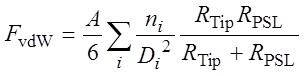
ここで,Diはi番目のPSL粒子とAFM探針間の距離で, niは距離Diに存在するPSL粒子の数である。表面間距離Diと最小表面間距離D0の比(Di/D0)をciとすると
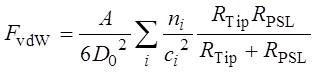
で表わされる。
AFM探針とPSL粒子の最小表面間距離D0の最小値は,vdW半径程度と考えられるため,表面間距離D0の最小値は0.4nm程度とした。上式に基づく隣接する各PSL粒子を考慮した相互作用力のPSL粒径依存性を下図 (a), (b)に示す。下図 (a)のように,隣接するPSL粒子の影響の項(![]() )は,PSL粒子の粒径が20nm以下になると,PSL粒子の粒径の減少に伴い増加している。その結果,相互作用力も,PSL粒子の粒径20nm以下で増加している。これは,PSL粒子の粒径が無限小において最密充填している場合の極限,およびPSL粒子の粒径が無限大に増加したときの極限が,共に平面として近似されることを意味している。また下図(b)にあるように,表面間距離D0が長くなるに従って相互作用力は小さくなるが,下図中に示した付着力の極小点PにおけるPSL粒子の粒径が大きくなっている。これは,粒子表面の凹凸に対し表面間距離D0が大きくなった為,相対的に表面凹凸の影響が減少した為と考えられる。ジャンプインはAFM探針とPSL粒子が離れている際に生じることから,表面間距離D0はジャンプアウトに比べ大きいと考えられる。実測値に対するカーブフィットを下図にて行った。これより,ジャンプイン時の近距離引力の値は, D0=4nmにおいてシミュレーションした相互作用力のPSL粒径依存性とほぼ一致した。従って,ジャンプイン時の近距離引力には,隣接しているPSL粒子の相互作用の影響が強く反映されていることが考えられる。
)は,PSL粒子の粒径が20nm以下になると,PSL粒子の粒径の減少に伴い増加している。その結果,相互作用力も,PSL粒子の粒径20nm以下で増加している。これは,PSL粒子の粒径が無限小において最密充填している場合の極限,およびPSL粒子の粒径が無限大に増加したときの極限が,共に平面として近似されることを意味している。また下図(b)にあるように,表面間距離D0が長くなるに従って相互作用力は小さくなるが,下図中に示した付着力の極小点PにおけるPSL粒子の粒径が大きくなっている。これは,粒子表面の凹凸に対し表面間距離D0が大きくなった為,相対的に表面凹凸の影響が減少した為と考えられる。ジャンプインはAFM探針とPSL粒子が離れている際に生じることから,表面間距離D0はジャンプアウトに比べ大きいと考えられる。実測値に対するカーブフィットを下図にて行った。これより,ジャンプイン時の近距離引力の値は, D0=4nmにおいてシミュレーションした相互作用力のPSL粒径依存性とほぼ一致した。従って,ジャンプイン時の近距離引力には,隣接しているPSL粒子の相互作用の影響が強く反映されていることが考えられる。
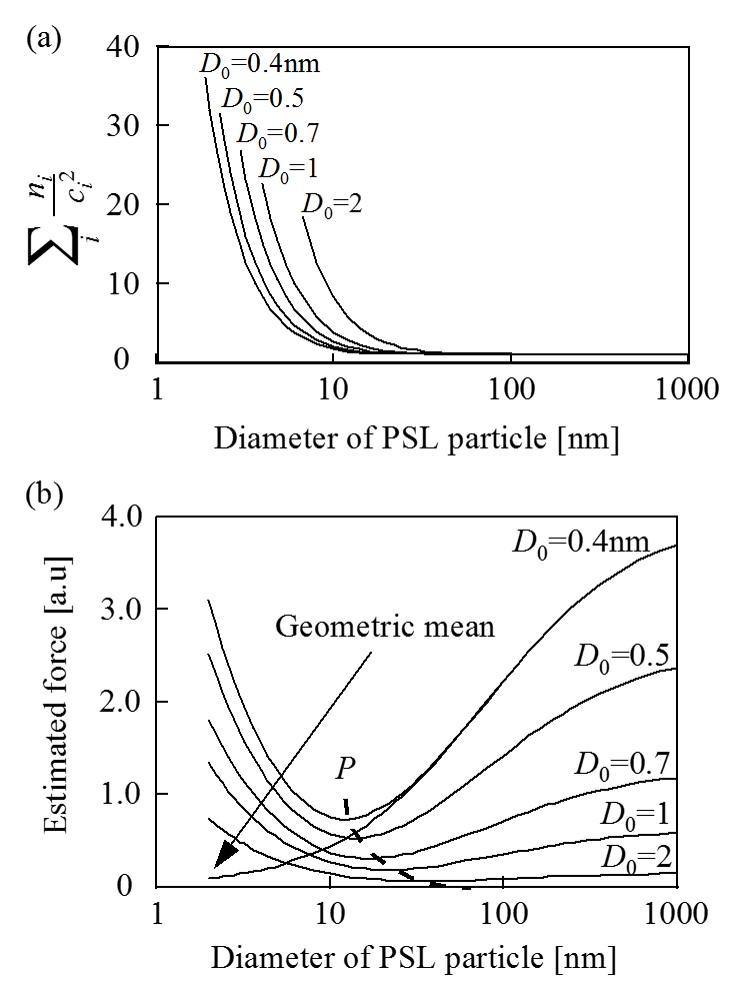
一方,ジャンプアウトが起きる表面間距離D0は,前述のように0.4nm程度と考えられる。上図(b) のシミュレーション結果で,D0=0.4nmにおける補正された幾何平均半径のPSL粒径依存性は,PSL粒子の粒径が20nmまで幾何平均半径と同じである。従って,下図のように,粒径20nm以上のPSL粒子とAFM探針間に作用するジャンプアウト時の付着力は,隣接しているPSL粒子の相互作用の影響は小さく,PSL粒子の接触変形の影響が支配的であると考えられる。PSL粒子の変形および隣接しているPSL粒子の影響の他に考慮すべき点として,分子レベルでの凹凸(ミニチップ)の影響,AFM探針先端の球近似の限界などが考えられる。
AFM探針とPSL凝集粒子間に作用する付着力と近距離引力をフォースカーブを用いて測定し,PSL粒子の粒径依存性に与えるPSL粒子の変形の寄与と隣接粒子の影響について解析した。ここで,微粒子系での力の粒径依存性の観点からDMT理論によるvdW力の幾何平均半径の補正を提案した。ジャンプアウト時の付着力は,AFM探針との接触により変形したPSL粒子の半径を1.7倍と補正することで,DMT理論式により理解できた。一方,ジャンプイン時の近距離引力は,隣接している周囲のPSL粒子とAFM探針との相互作用の影響を考慮した補正式により理解できた。実際の半導体表面への微粒子付着現象の解析にも有効な知見を与えている。